题目内容
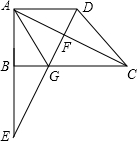
 已知:如图,直角△ABC中,∠ABC=90°,将△ABC绕着顶点C按顺时针方向旋转角度α(0<α<180°) 得到△A′B′C,连接AA′,BB′,射线 BB′交AC于点M,交AA′于点N
已知:如图,直角△ABC中,∠ABC=90°,将△ABC绕着顶点C按顺时针方向旋转角度α(0<α<180°) 得到△A′B′C,连接AA′,BB′,射线 BB′交AC于点M,交AA′于点N(1)若AC=6
| 3 |
(2)求证:△AMN∽△BMC
(3)若3AN=4B′C,sin∠BAC=
| 1 |
| 4 |
分析:(1)首先根据旋转的性质得到CB=CB',然后根据等腰三角形的性质得到∠CBB′=∠CB′B=
=90-
,
而∠BAC=
,∠ABC=90°,由此得到∠BCM=90°-
,接着得到∠CBB'=∠BCM,所以BM=CM,又∵∠BAC=∠ABM,所以有AM=BM,∴这样BM是Rt△ABC斜边上的中线,由此即可求出BM的长度;
(2)首先由(1)得到∠CBB′=∠CB′B=
=90-
,而∠CAA′=90-
,所以∠CAA'=∠CBB',又∠AMN=∠BMC,然后利用相似三角形的判定定理即可证明△AMN∽△BMC;
(3)根据相似三角形的性质可以得到
=
=
=
,过点M画MH⊥AB于H,而sin∠BAC=
,由此得到MH=
AM,在Rt△BHM中,sin∠MBH=
AM÷
AM=
,由此即可确定旋转角α的度数.
| 180-α |
| 2 |
| α |
| 2 |
而∠BAC=
| α |
| 2 |
| α |
| 2 |
(2)首先由(1)得到∠CBB′=∠CB′B=
| 180-α |
| 2 |
| α |
| 2 |
| α |
| 2 |
(3)根据相似三角形的性质可以得到
| AM |
| BM |
| AN |
| BC |
| AN |
| B′C |
| 4 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
解答:解:(1)∵CB=CB',
∴∠CBB′=∠CB′B=
=90-
.
∵∠BAC=
,∠ABC=90°,
∴∠BCM=90°-
.
∴∠CBB'=∠BCM.
∴BM=CM.
又∵∠BAC=∠ABM,
∴AM=BM.(2分)
∴BM是Rt△ABC斜边上的中线,
∴BM=
AC=3
.(3分)
(2)∵CB=CB',
∴∠CBB′=∠CB′B=
=90-
.
同理∠CAA′=90-
,
∴∠CAA'=∠CBB'.(5分)
又∠AMN=∠BMC,
∴△AMN∽△BMC.(6分)
 (3)∵△AMN∽△BMC.
(3)∵△AMN∽△BMC.
∴
=
=
=
.(7分)
过点M画MH⊥AB于H,
∵sin∠BAC=
,
∴MH=
AM.
在Rt△BHM中,sin∠MBH=
AM÷
AM=
.(8分)
∴∠ABM=19.5°.
∴∠CBB'=∠CB'B=90°-19.5°=70.5°,
∴α=180°-70.5×2=39°.(10分)
∴∠CBB′=∠CB′B=
| 180-α |
| 2 |
| α |
| 2 |
∵∠BAC=
| α |
| 2 |
∴∠BCM=90°-
| α |
| 2 |
∴∠CBB'=∠BCM.
∴BM=CM.
又∵∠BAC=∠ABM,
∴AM=BM.(2分)
∴BM是Rt△ABC斜边上的中线,
∴BM=
| 1 |
| 2 |
| 3 |
(2)∵CB=CB',
∴∠CBB′=∠CB′B=
| 180-α |
| 2 |
| α |
| 2 |
同理∠CAA′=90-
| α |
| 2 |
∴∠CAA'=∠CBB'.(5分)
又∠AMN=∠BMC,
∴△AMN∽△BMC.(6分)
 (3)∵△AMN∽△BMC.
(3)∵△AMN∽△BMC.∴
| AM |
| BM |
| AN |
| BC |
| AN |
| B′C |
| 4 |
| 3 |
过点M画MH⊥AB于H,
∵sin∠BAC=
| 1 |
| 4 |
∴MH=
| 1 |
| 4 |
在Rt△BHM中,sin∠MBH=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
∴∠ABM=19.5°.
∴∠CBB'=∠CB'B=90°-19.5°=70.5°,
∴α=180°-70.5×2=39°.(10分)
点评:此题分别考查了旋转的性质、相似三角形的判定与性质、直角三角形斜边上的中线的性质及三角函数的定义,综合性比较强,要求学生对于这些基础知识必须熟练掌握才能很好解决问题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 已知:如图,直角△ABC中,∠ACB=90°,AC=BC=1,
已知:如图,直角△ABC中,∠ACB=90°,AC=BC=1,
 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为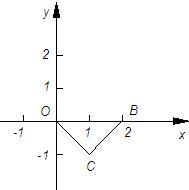 26、已知,如图,直角坐标系中,OC=BC,∠OCB=90°,点B(2,0).
26、已知,如图,直角坐标系中,OC=BC,∠OCB=90°,点B(2,0).