题目内容
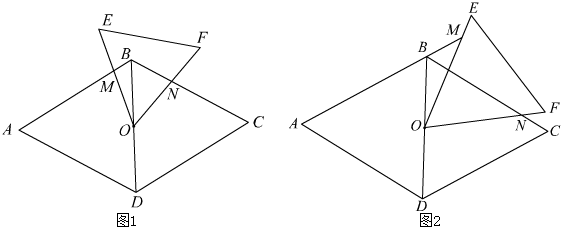
如图1,已知点O为菱形ABCD的对角线的交点,∠A=60°,将等边△OEF的顶点放在O处,直线OE、OF分别交直线AB、BC于M、N.
(1)求证:ON=OM.
(2)写出线段BM,BN与AB之间的数量关系并证明;
(3)将图1中的△OEF绕点O顺时针旋转至图2的位置,请直接写出线段BM,BN与AB之间的数量关系.

(1)求证:ON=OM.
(2)写出线段BM,BN与AB之间的数量关系并证明;
(3)将图1中的△OEF绕点O顺时针旋转至图2的位置,请直接写出线段BM,BN与AB之间的数量关系.
考点:菱形的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)取BC的中点G,连接OG,证明△OBM≌△OGN,根据全等三角形的对应边相等即可证得;
(2)同(1)的方法取BC中点G,同理可证:△OBM≌△OGN即可得到;
(3)同(1)的方法取BC中点G,延长AB交OE于点H,先证明BH=BM,再同理可证:△OBM≌△OGN即可得到.
(2)同(1)的方法取BC中点G,同理可证:△OBM≌△OGN即可得到;
(3)同(1)的方法取BC中点G,延长AB交OE于点H,先证明BH=BM,再同理可证:△OBM≌△OGN即可得到.
解答: (1)证明:取BC的中点G,连接OG,
(1)证明:取BC的中点G,连接OG,
∵四边形ABCD是菱形,∠A=60°
∴∠A=∠C=∠ABD=60°,AB=BC=CD=DA,
∵点O为菱形ABCD的对称中心,
∴OD=OB
∴OG∥CD
∴∠BGO=∠C=60°,OG=OB
∵△OEF是等边三角形,
∴∠EOF=60°,
∴∠BOM=∠NOG
又∵∠BGO=∠ABD=60°
在△OBM和△OGN中,
,
∴△OBM≌△OGN(ASA),
∴OM=ON;
(2)BN+BM=
AB,证明如下:
取BC中点G,
同理可证:△OBM≌△OGN,
∴BM=GN,
∴BG=BN+NG,
∴BN+BM=BG=
AB;
(3)BN-BM=
AB,证明如下:
取BC中点G,同理可证得△OBM≌△OGN,
∴BM=GN,
∴BG=BN-NG,
∴BN-BM=BG=
AB.
 (1)证明:取BC的中点G,连接OG,
(1)证明:取BC的中点G,连接OG,∵四边形ABCD是菱形,∠A=60°
∴∠A=∠C=∠ABD=60°,AB=BC=CD=DA,
∵点O为菱形ABCD的对称中心,
∴OD=OB
∴OG∥CD
∴∠BGO=∠C=60°,OG=OB
∵△OEF是等边三角形,
∴∠EOF=60°,
∴∠BOM=∠NOG
又∵∠BGO=∠ABD=60°
在△OBM和△OGN中,
|
∴△OBM≌△OGN(ASA),
∴OM=ON;
(2)BN+BM=
| 1 |
| 2 |
取BC中点G,
同理可证:△OBM≌△OGN,
∴BM=GN,
∴BG=BN+NG,
∴BN+BM=BG=
| 1 |
| 2 |
(3)BN-BM=
| 1 |
| 2 |
取BC中点G,同理可证得△OBM≌△OGN,
∴BM=GN,
∴BG=BN-NG,
∴BN-BM=BG=
| 1 |
| 2 |
点评:本题考查了全等三角形的全等的判定与性质,证明线段相等的问题常用的方法是转化为证三角形全等,正确作出辅助线是关键.

练习册系列答案
相关题目
计算3-
的结果是( )
| 9 |
| A、0 | B、-1 | C、6 | D、-6 |
若数轴上的点A向左移动2个单位长度,再向右移动3个单位长度,正好对应-5这个点,那么原来A点对应的数是( )
| A、-4 | B、2 | C、-6 | D、0 |