题目内容
在数轴上A、B两点分别表示有理数-1和x,我们用|AB|表示A、B两点之间的距离

(1)当|AB|=4时,x的值为______.
(2)当x=7时,点A,B分别以每秒1个单位长度和2个单位长度的速度同时向数轴负方向运动,求经过多少秒后,点A到原点的距离是点B到原点的距离的2倍.
解:(1)∵在数轴上A、B两点分别表示有理数-1和x,
∴当|AB|=4时,x+1=4或x+1=-4,
解得:x=-5或x=3;
故答案为:-5或3;
(2)设经过t秒后点A到原点的距离是点B到原点的距离的2倍.
第一种情况:t+1=2(7-2t)
解得:t=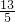 =2.6,
=2.6,
第二种情况:t+1=2(2t-7)
解得:t=5,
答:经过2.6秒或5秒后,点A到原点的距离是点B到原点的距离的2倍.
分析:(1)根据当|AB|=4时,x+1=4或x+1=-4,进而求出x的值即可;
(2)根据第一种情况:t+1=2(7-2t)以及第二种情况:t+1=2(2t-7)分别求出即可.
点评:此题主要考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
∴当|AB|=4时,x+1=4或x+1=-4,
解得:x=-5或x=3;
故答案为:-5或3;
(2)设经过t秒后点A到原点的距离是点B到原点的距离的2倍.
第一种情况:t+1=2(7-2t)
解得:t=
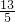 =2.6,
=2.6,第二种情况:t+1=2(2t-7)
解得:t=5,
答:经过2.6秒或5秒后,点A到原点的距离是点B到原点的距离的2倍.
分析:(1)根据当|AB|=4时,x+1=4或x+1=-4,进而求出x的值即可;
(2)根据第一种情况:t+1=2(7-2t)以及第二种情况:t+1=2(2t-7)分别求出即可.
点评:此题主要考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

