题目内容
 (2012•虹口区一模)已知二次函数y=-
(2012•虹口区一模)已知二次函数y=-| 1 |
| 2 |
| 5 |
| 2 |
(1)用配方法求出该函数图象的顶点坐标和对称轴;
(2)在平面直角坐标系中画出该函数的大致图象.
分析:(1)利用配方法求出二次函数的对称轴和顶点坐标即可;
(2)把握抛物线与x轴,y轴的交点,顶点坐标,开口方向等画出图象即可.
(2)把握抛物线与x轴,y轴的交点,顶点坐标,开口方向等画出图象即可.
解答:解:(1)
y=-
x2+3x-
=-
(x2-6x)-
=-
(x2-6x+9-9)-
=-
(x-3)2+2,
故顶点坐标为(3,2)和对称轴为直线x=3;
(2)当y=0,则0=-
(x-3)2+2,解得:x=1或x=5,则图象与x轴的交点坐标为:(1,0),(5,0),
当x=0,则y=-
,则图象与y轴的交点坐标为:(0,-
),如图所示:
 .
.
y=-
| 1 |
| 2 |
| 5 |
| 2 |
=-
| 1 |
| 2 |
| 5 |
| 2 |
=-
| 1 |
| 2 |
| 5 |
| 2 |
=-
| 1 |
| 2 |
故顶点坐标为(3,2)和对称轴为直线x=3;
(2)当y=0,则0=-
| 1 |
| 2 |
当x=0,则y=-
| 5 |
| 2 |
| 5 |
| 2 |
 .
.点评:此题主要考查了配方法求二次函数的对称轴和顶点坐标,此题是二次函数的基本性质也是考查重点,同学们应熟练掌握.

练习册系列答案
相关题目
 (2012•虹口区一模)如图,分别以下列选项作为一个已知条件,其中不一定能得到△AOB∽△COD的是( )
(2012•虹口区一模)如图,分别以下列选项作为一个已知条件,其中不一定能得到△AOB∽△COD的是( )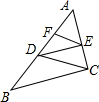 (2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( )
(2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( )