题目内容
 (2012•杨浦区二模)已知抛物线y=ax2-x-c过点A(-6,0),与y轴交于点B,顶点为D,对称轴是直线x=-2.
(2012•杨浦区二模)已知抛物线y=ax2-x-c过点A(-6,0),与y轴交于点B,顶点为D,对称轴是直线x=-2.(1)求此抛物线的表达式及点D的坐标;
(2)连接DO,求证:∠AOD=∠ABO;
(3)点P在y轴上,且△ADP与△AOB相似,求点P的坐标.
分析:(1)将对称轴是直线x=-2,以及点A(-6,0),代入解析式求出即可;
(2)过D作DH⊥x轴,利用D(-2,4),得出在Rt△DHO中tan∠AOD=2,进而得出∠AOD=∠ABO;
(3)分别根据情况1:若∠DAP=90°,情况2:若∠ADP=90°,情况3:若∠APD=90°,分析得出P点坐标即可.
(2)过D作DH⊥x轴,利用D(-2,4),得出在Rt△DHO中tan∠AOD=2,进而得出∠AOD=∠ABO;
(3)分别根据情况1:若∠DAP=90°,情况2:若∠ADP=90°,情况3:若∠APD=90°,分析得出P点坐标即可.
解答: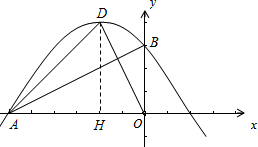 解:(1)由题意得
解:(1)由题意得
,
解得
,
∴抛物线的表达式为y=-
x2-x+3,
顶点D坐标为(-2,4);
(2)过D作DH⊥x轴,
∵D(-2,4),
∴在Rt△DHO中tan∠AOD=2,
又∵B(0,3),A(-6,0),
∴在Rt△ABO中tan∠ABO=2,
∴∠AOD=∠ABO;
(3)∵△ADP与△AOB相似,而△AOB为直角三角形,
∴△ADP也为直角三角形,
∴情况1:若∠DAP=90°,
∵D(-2,4),A(-6,0),
∴∠DAO=45°,∴∠OAP=45°,
∴P(0,-6)
但此时AD=4
,AP=6
,
∴
=
,又
=
,
∴△ADP与△AOB不相似,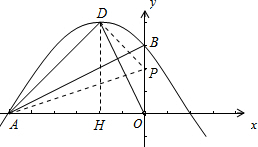
∴此时点P不存在.
情况2:若∠ADP=90°,
∵D(-2,4),A(-6,0),
∴∠ADH=45°,∴∠HDP=45°,
∴P(0,2)
此时,
=
=
,
=
,且∠ADP=∠AOB,
∴△ADP与△AOB相似,
即当P(0,2)时,使得△ADP与△AOB相似.
情况3:若∠APD=90°,设P(0,t),
则AP2+PD2=AD2,
即36+t2+4+(t-4)2=32,得t2-4t+12=0,
∵△<0,
∴无解,
∴点P不存在.
综上所述,点P的坐标是(0,2).
 解:(1)由题意得
解:(1)由题意得
|
解得
|
∴抛物线的表达式为y=-
| 1 |
| 4 |
顶点D坐标为(-2,4);
(2)过D作DH⊥x轴,
∵D(-2,4),
∴在Rt△DHO中tan∠AOD=2,
又∵B(0,3),A(-6,0),
∴在Rt△ABO中tan∠ABO=2,
∴∠AOD=∠ABO;
(3)∵△ADP与△AOB相似,而△AOB为直角三角形,
∴△ADP也为直角三角形,
∴情况1:若∠DAP=90°,
∵D(-2,4),A(-6,0),
∴∠DAO=45°,∴∠OAP=45°,
∴P(0,-6)
但此时AD=4
| 2 |
| 2 |
∴
| AD |
| AP |
| 2 |
| 3 |
| OB |
| AO |
| 1 |
| 2 |
∴△ADP与△AOB不相似,

∴此时点P不存在.
情况2:若∠ADP=90°,
∵D(-2,4),A(-6,0),
∴∠ADH=45°,∴∠HDP=45°,
∴P(0,2)
此时,
| DP |
| AD |
2
| ||
4
|
| 1 |
| 2 |
| OB |
| AO |
| 1 |
| 2 |
∴△ADP与△AOB相似,
即当P(0,2)时,使得△ADP与△AOB相似.
情况3:若∠APD=90°,设P(0,t),
则AP2+PD2=AD2,
即36+t2+4+(t-4)2=32,得t2-4t+12=0,
∵△<0,
∴无解,
∴点P不存在.
综上所述,点P的坐标是(0,2).
点评:此题主要考查了待定系数法求二次函数解析式以及相似三角形的性质与判定,以及分类讨论思想的应用,根据△ADP不同角为90度分别得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•杨浦区二模)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(2012•杨浦区二模)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.