Question

类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（）=1．

    　　若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为．

    解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．

  （2）①动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”

{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”

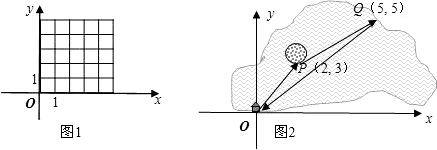
{3，1}平移，最后的位置还是点B吗? 在图1中画出四边形OABC.

②证明四边形OABC是平行四边形.

（3）如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O. 请用“平移量”加法算式表示它的航行过程．

Answer 1

解：（1）{3，1}+{1，2}={4，3}．  

{1，2}+{3，1}={4，3}．

（2）①画图

（3）存在，过点D作DM⊥AE交AB于点M，则此时M使得四边  形DMEP是平行四边形。证明如下：

    ∵DM⊥AE，∴∠ADM=90°－∠DAE。

    ∵四边形ABCD为正方形，

∴AB=AD，∠B=∠BAD=90°。

 ∴∠BAE=90°－∠DAE。∴∠BAE=∠ADM。

    ∴△BAE≌△ADM（ASA）。∴AD=DM。

    由（2）AE=EP，得DM= EP。

   又∵DM⊥AE，AE⊥EF，∴DM∥ EP。∴四边形DMEP是平行四边形。