��Ŀ����
��6�֣����ѧϰ��һ����������������ƽ��3����λ��������ƽ��2����λ���൱������ƽ��1����λ����ʵ���ӷ���ʾΪ 3+��![]() ��=1��������ƽ���ϵĵ�������ƽ�ƣ���x�᷽��ƽ�Ƶ�����Ϊa������Ϊ��������Ϊ����ƽ��
��=1��������ƽ���ϵĵ�������ƽ�ƣ���x�᷽��ƽ�Ƶ�����Ϊa������Ϊ��������Ϊ����ƽ��![]() ����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ��
����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ��![]() ����λ���������������{a��b}������һƽ�Ƶġ�ƽ����������ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ
����λ���������������{a��b}������һƽ�Ƶġ�ƽ����������ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ![]() ��
��

������⣺
1.��1�����㣺{3��1}+{1��2}��{1��2}+{3��1}��
2.��2���ٶ���P������ԭ��O�������Ȱ��ա�ƽ������{3��1}ƽ�Ƶ�A���ٰ��ա�ƽ������
{1��2}ƽ�Ƶ�B�����ȰѶ���P���ա�ƽ������{1��2}ƽ�Ƶ�C���ٰ��ա�ƽ������
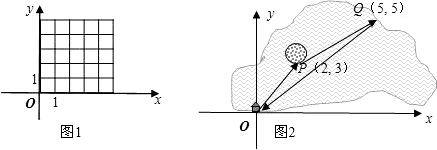
{3��1}ƽ�ƣ�����λ�û��ǵ�B��? ��ͼ1�л����ı���OABC.
��֤���ı���OABC��ƽ���ı���.
3.��3����ͼ2��һ�Ҵ�����ͷO�������Ⱥ��е����ĵ���ͷP��2��3�����ٴ���ͷP���е���ͷQ��5��5�������ص�������O. ���á�ƽ�������ӷ���ʽ��ʾ���ĺ��й��̣�
1.��1��{3��1}+{1��2}={4��3}��
{1��2}+{3��1}={4��3}��
2.��2���ٻ�ͼ 
���������B
�� ֤�����ɢ�֪��A��3��1����B(4��3)��C��1��2��
��OC=AB=![]() =
=![]() ��OA=BC=
��OA=BC=![]() =
=![]() ��
��
���ı���OABC��ƽ���ı���
3.��3��{2��3}+{3��2}+{-5��-5}={0,0}��
����:��

 �л����ı���OABC��
�л����ı���OABC�� ��=1��
��=1�� ����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ��
����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ�� ����λ���������������{a��b}������һƽ�Ƶġ�ƽ����������ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ
����λ���������������{a��b}������һƽ�Ƶġ�ƽ����������ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ ��
��
 ��=1��������ƽ���ϵĵ�������ƽ�ƣ���x�᷽��ƽ�Ƶ�����Ϊa������Ϊ��������Ϊ����ƽ��
��=1��������ƽ���ϵĵ�������ƽ�ƣ���x�᷽��ƽ�Ƶ�����Ϊa������Ϊ��������Ϊ����ƽ�� ����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ��
����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ�� ����λ���������������{a��b}������һƽ�Ƶġ�ƽ����������ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ
����λ���������������{a��b}������һƽ�Ƶġ�ƽ����������ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ ��
��