题目内容
 如图,PA、PB是⊙O的两条切线,切点是A、B,如果OP=4,∠APB=60°,那么⊙O的半径是________.
如图,PA、PB是⊙O的两条切线,切点是A、B,如果OP=4,∠APB=60°,那么⊙O的半径是________.
2
分析:根据切线的性质求得∠APO=30°,∠PAO=90°,再由直角三角形的性质得AO=2.
解答:∵PA、PB是⊙O的两条切线,
∴∠APO=∠BPO= ∠APB,∠PAO=90°,
∠APB,∠PAO=90°,
∵∠APB=60°,
∴∠APO=30°,
∵PO=4,
∴AO=2.
故答案为:2.
点评:本题考查了切线长定理、切线的性质和直角三角形的性质,是基础知识要熟练掌握.
分析:根据切线的性质求得∠APO=30°,∠PAO=90°,再由直角三角形的性质得AO=2.
解答:∵PA、PB是⊙O的两条切线,
∴∠APO=∠BPO=
 ∠APB,∠PAO=90°,
∠APB,∠PAO=90°,∵∠APB=60°,
∴∠APO=30°,
∵PO=4,
∴AO=2.
故答案为:2.
点评:本题考查了切线长定理、切线的性质和直角三角形的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
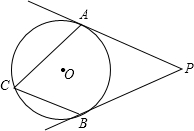 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
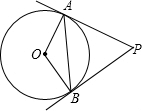 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于