题目内容
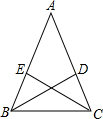
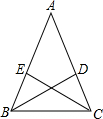 证明命题:“等腰三角形两底角的平分线相等.”是真命题.
证明命题:“等腰三角形两底角的平分线相等.”是真命题.
已知:如图,在△ABC中,AB=________,BD,CE分别∠ABC,∠ACB的角平分线.
求证:________.
证明:
AC BD=CE
分析:求出∠ABC=∠ACB,∠ECB=∠DBC,证△BCE≌△CBD,根据全等三角形的性质推出即可.
解答:已知:在△ABC中,AB=AC,BD,CE分别是∠ABC和∠ACB的角平分线,
求证:BD=CE
证明:∵AB=AC(已知)
∴∠ABC=∠ACB(在同一个三角形中,等边对等角),
∵BD,CE分别∠ABC,∠ACB的角平分线.
∴∠CBD= ∠ABC,∠BCE=
∠ABC,∠BCE= ∠ACB(角平分线的定义).
∠ACB(角平分线的定义).
即:∠BCE=∠CBD,
∵在△BCE和△CBD中,
 ,
,
∴△BCE≌△CBD(ASA),
∴BD=CE(全等三角形,对应边相等).
∴“等腰三角形两底角的平分线相等”是真命题.
故答案为:AC、BD=CE.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,关键是推出△BCE≌△CBD.
分析:求出∠ABC=∠ACB,∠ECB=∠DBC,证△BCE≌△CBD,根据全等三角形的性质推出即可.
解答:已知:在△ABC中,AB=AC,BD,CE分别是∠ABC和∠ACB的角平分线,
求证:BD=CE
证明:∵AB=AC(已知)
∴∠ABC=∠ACB(在同一个三角形中,等边对等角),
∵BD,CE分别∠ABC,∠ACB的角平分线.
∴∠CBD=
 ∠ABC,∠BCE=
∠ABC,∠BCE= ∠ACB(角平分线的定义).
∠ACB(角平分线的定义).即:∠BCE=∠CBD,
∵在△BCE和△CBD中,
 ,
,∴△BCE≌△CBD(ASA),
∴BD=CE(全等三角形,对应边相等).
∴“等腰三角形两底角的平分线相等”是真命题.
故答案为:AC、BD=CE.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,关键是推出△BCE≌△CBD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题宜用反证法证明的是( )
| A、等腰三角形两腰上的高相等 | B、有一个外角是1200的等腰三角形是等边三角形 | C、两条直线都与第三条直线平行,则这两条直线互相平行 | D、全等三角形的面积相等 |
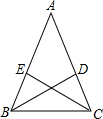 证明命题:“等腰三角形两底角的平分线相等.”是真命题.
证明命题:“等腰三角形两底角的平分线相等.”是真命题.