题目内容
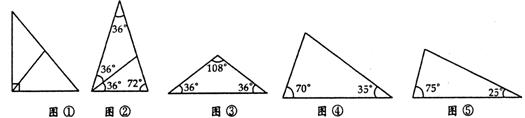
顶角为36°的等腰三角形称为黄金三角形，如图，△ABC，△BDC，△DEC都是黄金三角形，己知AB=2cm，则DE=分析：黄金三角形是一个等腰三角形，它的顶角为36°，每个底角为72°．它的腰与它的底成黄金比．当底角被平分时，角平分线分对边也成黄金比，并形成两个较小的等腰三角形．这两三角形之一相似于原三角形．
解答：解：△ABC为黄金三角形，△BDC为黄金三角形，△DEC为黄金三角形
有AB=AC，BD=BC=AD，DE=CD，
且△ABC∽△BDC，
有BC2=AB•CD
AB=2，
则有CD=
BC2=
AD2①
CD+AD=AC=2②
则AD=2-CD③代入①整理得
CD2-6CD+4=0
解得CD=3±
CD=3+
＞1，舍去
得CD=3-
DE=CD
故DE=3-
．
有AB=AC，BD=BC=AD，DE=CD，
且△ABC∽△BDC，
有BC2=AB•CD
AB=2，
则有CD=
| 1 |
| 2 |
| 1 |
| 2 |
CD+AD=AC=2②
则AD=2-CD③代入①整理得
CD2-6CD+4=0
解得CD=3±
| 5 |
CD=3+
| 5 |
得CD=3-
| 5 |
DE=CD
故DE=3-
| 5 |
点评：黄金三角形的一个几何特征是：它是唯一一种能够由5个与其全等的三角形生成其相似三角形的三角形．
练习册系列答案
相关题目
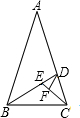如图所示，顶角为36°的等腰三角形，其底边与腰之比等于k，这样的三角形叫黄金三角形，已知腰长AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2007个黄金三角形的周长为（ ）| A、k2006 | ||
| B、k2007 | ||
C、
| ||
| D、k2006（2+k） |
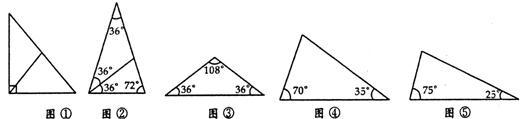
20、已知：△ABC与△CDE都是顶角为36°的等腰三角形，BC=CD，AC与BD交于F，且B、C、E三点共线．
如图所示，顶角为36°的等腰三角形，其底边与腰之比等于k，这样的三角形叫做黄金三角形．已知AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2014个黄金三角形的周长为（ ）