题目内容
在△ABC中,∠ABC=∠C,直线MN是AB的垂直平分线,MN与AB相交于点D,与AC所在直线相交于E点,若∠AED=40°,求∠EBC的度数.
考点:线段垂直平分线的性质
专题:
分析:此题根据△ABC中∠A为锐角与钝角分两种情况进行解答.
解答: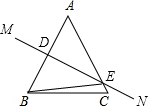 解:(1)当AB的中垂线MN与AC边相交时,
解:(1)当AB的中垂线MN与AC边相交时,
∵∠ADE=90°,
∴∠A=90°-40°=50°,
∵AE=BE,
∴∠ABE=∠A=50°,
∴∠ABC=∠C=
(180°-∠A)=65°,
 ∴∠EBC=∠ABC-∠ABE=15°;
∴∠EBC=∠ABC-∠ABE=15°;
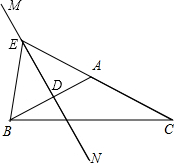
(2)当AB的中垂线MN与CA的延长线相交时,
∴∠DAE=90°-40°=50°,
∵AE=BE,
∴∠ABE=∠DAE=50°,
∴∠ABC=∠C=
∠DAE=25°,
∴∠EBC=∠ABC+∠ABE=75°.
 解:(1)当AB的中垂线MN与AC边相交时,
解:(1)当AB的中垂线MN与AC边相交时,∵∠ADE=90°,
∴∠A=90°-40°=50°,
∵AE=BE,
∴∠ABE=∠A=50°,
∴∠ABC=∠C=
| 1 |
| 2 |
 ∴∠EBC=∠ABC-∠ABE=15°;
∴∠EBC=∠ABC-∠ABE=15°;(2)当AB的中垂线MN与CA的延长线相交时,
∴∠DAE=90°-40°=50°,
∵AE=BE,
∴∠ABE=∠DAE=50°,
∴∠ABC=∠C=
| 1 |
| 2 |
∴∠EBC=∠ABC+∠ABE=75°.
点评:本题考查的是线段垂直平分线的性质,等腰三角形的性质,三角形内角和定理及外角的性质,此类题需要注意的是要分两种情况解答,考生在考虑问题时要全面.

练习册系列答案
相关题目
一元二次方程x2+7x+a=0中,a<0,该方程的解的情况是( )
| A、没有实数根 |
| B、有两个不相等的实数根 |
| C、有两个相等的实数根 |
| D、不能确定 |
已知一次函数y=kx-3,已知当x=-5时,y=7,那么k的值是( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
下列说法中不正确的是( )
| A、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直 |
| B、从直线外一点到这条直线的垂线段叫做点到直线的距离 |
| C、一条直线的垂线可以画无数条 |
| D、连接直线外一点与直线上各点的所有线段中,垂线段最短 |
 如图,在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒的影子是BE.
如图,在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着,其中AB这根木棒的影子是BE.