题目内容
5.如图①,正方形AEFG的边长为1,正方形ABCD的边长为3,且点F在AD上.(1)求S△DBF;
(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的S△DBF;
(3)把正方形AEFG绕点A旋转一周,在旋转的过程中,S△DBF存在最大值与最小值,请直接写出最大值$\frac{15}{2}$,最小值$\frac{3}{2}$.
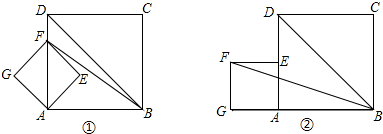
分析 (1)首先求出AF和BD的长,进而求出DF的长,利用三角形面积公式即可得到答案;
(2)连接AF,判断出△DFB与△ABD同底等高,求出△ABD的面积即可;
(3)F点的轨迹是以点A为圆心,AF为半径的圆,进而作出图形,故当F点到BD的距离取得最大、最小值时,S△BFD取得最大、最小值,结合图形求出最大值和最小值.
解答  解:(1)∵正方形ABCD的边长为3,
解:(1)∵正方形ABCD的边长为3,
∴BD=3$\sqrt{2}$,
∵正方形AEFG的边长为1,点F在AD上,
∴AF=$\sqrt{2}$,
∴DF=3-$\sqrt{2}$,
∴S△DBF=$\frac{1}{2}$×DF×AB=$\frac{1}{2}$×(3-$\sqrt{2}$)×3=$\frac{9}{2}$-$\frac{3\sqrt{2}}{2}$.
(2)连接AF,
∵AF是正方形AEFG的对角线,
BD是正方形ABCD的对角线,
∴AF∥BD,
∴△DFB与△ABD同底等高,
∴${S_{△DBF}}={S_{△ABD}}=\frac{9}{2}$.
(3)正方形AEFG在绕A点旋转的过程中,
F点的轨迹是以点A为圆心,AF为半径的圆,
因为△BFD的边BD=3$\sqrt{2}$,
故当F点到BD的距离取得最大、最小值时,S△BFD取得最大、最小值.
如图②当F点位于F1点时,S△BFD的最大值,最大值为$\frac{1}{2}$×($\sqrt{2}$+$\frac{3}{2}\sqrt{2}$)×3$\sqrt{2}$=$\frac{15}{2}$,
当F点位于F2点时,S△BFD取得最小值,最小值为$\frac{1}{2}$×($\frac{3\sqrt{2}}{2}$-$\sqrt{2}$)×3$\sqrt{2}$=$\frac{3}{2}$.
点评 本题考查了几何变换综合题的知识,涉及到旋转的性质、勾股定理及正方形的性质等中山市,解答本题要充分利用正方形的特殊性质,注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,解答第(3)问需要作出图形,数形结合很容易解决问题.

| A. | 扩大4倍 | B. | 扩大2倍 | C. | 不变 | D. | 缩小2倍 |
 如图,∠B=∠ADC=90°,AD=2DC,AB=BC=$\sqrt{6}$cm,求四边形ABCD的面积.
如图,∠B=∠ADC=90°,AD=2DC,AB=BC=$\sqrt{6}$cm,求四边形ABCD的面积.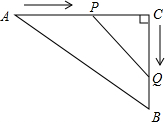 如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似?
如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似? 如图,已知C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形有3对,它们分别是△ACD与△BCE;△ACF与△BCG;△GEC与△FDC.
如图,已知C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形有3对,它们分别是△ACD与△BCE;△ACF与△BCG;△GEC与△FDC.