Question

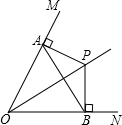如图，P为∠MON平分线上一点，PA⊥OM于A，PB⊥ON于B，
求证：OP垂直平分AB．

Answer 1

分析：根据角平分线性质得出PA=PB，根据HL证Rt△PAO≌Rt△PBO，推出OA=OB，根据等腰三角形性质推出即可．

解答：证明：∵P为∠MON平分线上一点，PA⊥OM，PB⊥ON，
∴PA=PB，∠PAO=∠PBO=90°，
在Rt△PAO和Rt△PBO中，

OP=OP PA=PB

，
∴Rt△PAO≌Rt△PBO（HL），
∴OA=OB，
∵OP平分∠AOB，
∴OP垂直平分AB（三线合一）．

点评：本题考查了全等三角形的性质和判定，角平分线性质，等腰三角形性质的应用，主要考查学生的推理能力．