题目内容
在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形,设正方形在直线y=x上方及直线y=-x+2a上方部分的面积为S.(1)求a=
| 1 | 2 |
(2)当a在实数范围内变化时,求S关于a的函数关系式.
分析:(1)由已知条件和题意,要求面积S的值,只要把三角形三个顶点坐标求出来问题就解决了;
(2)由题意知直线y=x是定的,而y=-x+2a是动的且平行于y=-x移动,此时面积S也是动的,从而要分类讨论,求出每种情况的面积表达式,根据几何关系及三角形顶点坐标易求S关于a的表达式.
(2)由题意知直线y=x是定的,而y=-x+2a是动的且平行于y=-x移动,此时面积S也是动的,从而要分类讨论,求出每种情况的面积表达式,根据几何关系及三角形顶点坐标易求S关于a的表达式.
解答:解:(1)当a=
时,如图1
直线y=x与y=-x+1的交点是E(
,
),
∴S=
×1×
=
. (2分)
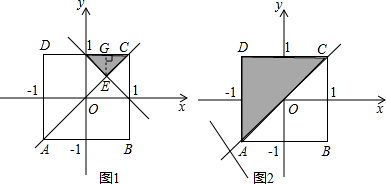
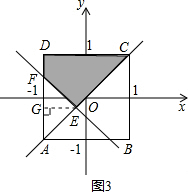
(2)①当a<-1时,如图2,△ADC的面积就是S.
∴S=
×2×2=2. (3分)
②当-1≤a<0时,如图3,直线y=x与y=-x+2a的交点是E(a,a),
∴EG=(1-|a|)=1+a AF=2(1+a),
∴S=S△ADC-S△AEF=2-
(1+a)×2(1+a)=2-(1+a)2.(6分)
③当0≤a<1时,如图4,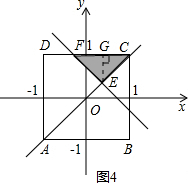
直线y=x与y=-x+2a的交点是E(a,a),
∴EG=1-a,CF=2(1-a),
∴S=S△CEF=
(1-a)×2(1-a)=(1-a)2(9分)
④当a≥1时,如图5,S=0. (11分)
∴S关于a的函数关系式为S=
.(12分)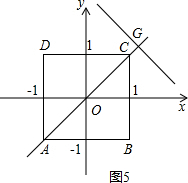
| 1 |
| 2 |
直线y=x与y=-x+1的交点是E(
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |


(2)①当a<-1时,如图2,△ADC的面积就是S.
∴S=
| 1 |
| 2 |
②当-1≤a<0时,如图3,直线y=x与y=-x+2a的交点是E(a,a),
∴EG=(1-|a|)=1+a AF=2(1+a),
∴S=S△ADC-S△AEF=2-
| 1 |
| 2 |
③当0≤a<1时,如图4,

直线y=x与y=-x+2a的交点是E(a,a),
∴EG=1-a,CF=2(1-a),
∴S=S△CEF=
| 1 |
| 2 |
④当a≥1时,如图5,S=0. (11分)
∴S关于a的函数关系式为S=
|

点评:此题看似复杂其实很简单,主要考查一次函数的性质及三角形的面积公式,还考查了直线的平移和分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
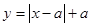 上侧部分的面积为S.当
上侧部分的面积为S.当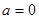 时,S= ▲ ;当
时,S= ▲ ;当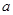 为任意实数时,面积S的最大值为 ▲ .
为任意实数时,面积S的最大值为 ▲ . 时,求S的值;
时,求S的值;