题目内容
在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形,设正方形在直线y1=x上方及直线y2=-x+2a上方部分的面积为S,
(1)当a= 时,求S的值;
时,求S的值;
(2)当a=0时,将两直线绕着原点O顺时针旋转20°,求S的值;
(3)a在实数范围内变化时,求S关于a的函数关系式.
 解:(1)当a=
解:(1)当a= 时,y2=-x+1,
时,y2=-x+1,如图1.
直线y1=x与直线y2=-x+1的交点是E(
 ,
, ),
),S=
 ×1×
×1× =
= ;
; (2)当a=0时,y2=-x,
(2)当a=0时,y2=-x,S=
 ×
× =
= ;
;(3)①当a<-1时,如图2,
△ADC的面积是S,
S=
 ×2×2=2;
×2×2=2; ②当-1≤a<0时,如图3,
②当-1≤a<0时,如图3,直线y=x与y=-x+2a的交点是E(a,a),
EG=(1-|a|)=1+a,
AF=2(1+a),
S=S△ADC-S△AEF
=2-
 (1+a)×2(1+a)
(1+a)×2(1+a) =2-(1+a)2;
=2-(1+a)2;③当0≤a<1时,如图4,
直线y=x与y=-x+2a的交点是E(a,a),
EG=1-a,
CF=2(1-a),
 S=S△CEF=
S=S△CEF= (1-a)×2(1-a)=(1-a)2;
(1-a)×2(1-a)=(1-a)2;④当a≥1时,如图5,S=0.
∴S关于a的函数关系式为:
①当a<-1时,S=2;②当-1≤a<0时,S=2-(1+a)2;③当0≤a<1时,S=(1-a)2;④当a≥1时,S=0.
分析:(1)当a=
 时,可得y2=-x+1,再根据三角形面积公式即可求解;
时,可得y2=-x+1,再根据三角形面积公式即可求解;(2)根据旋转的性质可知S的值等于大正方形面积的
 ;
;(3)分①当a<-1时;②当-1≤a<0时;③当0≤a<1时;④当a≥1时;四种情况讨论可求S关于a的函数关系式.
点评:本题考查了一次函数综合题,涉及的知识点有:图形的面积计算,旋转的性质,分类思想的运用,难度中等.

练习册系列答案
相关题目
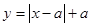 上侧部分的面积为S.当
上侧部分的面积为S.当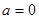 时,S= ▲ ;当
时,S= ▲ ;当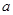 为任意实数时,面积S的最大值为 ▲ .
为任意实数时,面积S的最大值为 ▲ .