题目内容
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径r.
,求⊙O的半径r.

考点:
切线的判定.
分析:
(1)连接OA、OD,求出∠D+∠OFD=90°,推出∠CAF=∠CFA,∠OAD=∠D,求出∠OAD+∠CAF=90°,根据切线的判定推出即可;
(2)OD=r,OF=8﹣r,在Rt△DOF中根据勾股定理得出方程r2+(8﹣r)2=(![]() )2,求出即可.
)2,求出即可.
解答:
(1)证明:
连接OA、OD,
∵D为弧BE的中点,
∴OD⊥BC,
∠DOF=90°,
∴∠D+∠OFD=90°,
∵AC=AF,OA=OD,
∴∠CAF=∠CFA,∠OAD=∠D,
∵∠CFA=∠OFD,
∴∠OAD+∠CAF=90°,
∴OA⊥AC,
∵OA为半径,
∴AC是⊙O切线;
(2)解:∵⊙O半径是r,
当F在半径OE上时,
∴OD=r,OF=8﹣r,
在Rt△DOF中,r2+(8﹣r)2=(![]() )2,
)2,
r=![]() ,r=
,r=![]() (舍去);
(舍去);
当F在半径OB上时,
∴OD=r,OF=r﹣8,
在Rt△DOF中,r2+(r﹣8)2=(![]() )2,
)2,
r=![]() ,r=
,r=![]() (舍去);
(舍去);
即⊙O的半径r为![]() .
.
点评:
本题考查了切线的判定,等腰三角形的性质和判定,勾股定理等知识点的应用,主要考查学生的推理和计算的能力.

练习册系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.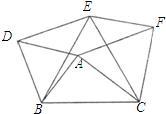 12、如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD、△BEC、△ACF.
12、如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD、△BEC、△ACF.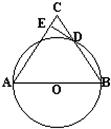 21、如图,以△ABC的边AB为直径作⊙O交BC于D,过D作⊙O的切线交AC于E,要使得DE⊥AC,则△ABC的边必须满足的条件是
21、如图,以△ABC的边AB为直径作⊙O交BC于D,过D作⊙O的切线交AC于E,要使得DE⊥AC,则△ABC的边必须满足的条件是 (2013•玉林)如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(2013•玉林)如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.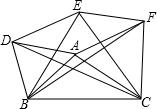 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF