Question

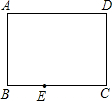如图，在正方形ABCD中，边长为2，某一点E从B-C-D-A-B运动，且速度是1，试求：
（1）△BEC的面积S和时间t的关系．
（2）作出S的图象．

Answer 1

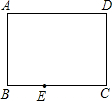解：（1）∵在正方形ABCD中，边长为2，某一点E从B-C-D-A-B运动，且速度是1，
∴当E在BC上时，B，E，C无法构成三角形，此时0≤t≤2，
∴S=0，（0≤t≤2）；
当E在CD上时，△BEC的面积为：S=BC×CE=×2×（t-2）=t-2，（2＜t≤4）；
当E在AD上时，△BEC的面积为：S=BC×CD=×2×2=2，（4＜t≤6）；
当E在Ab上时，△BEC的面积为：S=BC×BE=×2×[2-（t-6）]=8-t，（6＜t＜8）；

（2）根据（1）中解析式，以及t的取值范围求出S的值，
∴S=t-2中，∵2＜t≤4，∴t=2时，S=0，t=4时，S=2，在坐标系内找出（2，0），（4，2）即可得出它的图象；
∴S=8-t中，∵6＜t＜8，∴t=6时，S=2，t=8时，S=0，在坐标系内找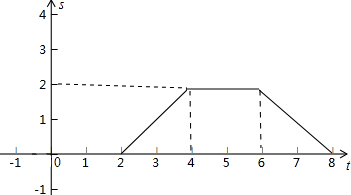出（6，2），（8，0）即可得出它的图象．
如图所示：
分析：（1）△BEC的面积可分为4部分讨论，分为当E在BC上时，当E在CD上时，当E在AD上时，当E在Ab上时，分别分析得出，因此对应的函数应为分段函数；
（2）根据利用自变量的取值范围分别得出对应函数值，从而画出图象．
点评：此题主要考查了动点函数图象问题，在图象中应注意自变量的取值范围，利用自变量的取值范围得出对应函数值，从而画出图象此题能够培养学生数形结合的综合能力．