题目内容
 (2012•盐城)如图所示,当小华站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°.若小华向后退0.5米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
(2012•盐城)如图所示,当小华站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°.若小华向后退0.5米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:| 3 |
分析:利用等腰直角三角形的性质得出AC=AA1,进而得出tan30°=
=
求出即可.
| BD |
| BB 1 |
| BD |
| AB+ A1B1+AA1 |
解答:解:∵当小华站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°.
∴AC=AA1,
∵若小华向后退0.5米到B处,这时他看自己的脚在镜中的像的俯角为30°,
∴AB=A1B1=0.5米,∠DB1B=30°,
∴tan30°=
=
=
=
,
解得:BD=
≈
≈1.4(米),
答:小华的眼睛到地面的距离为1.4米.
∴AC=AA1,
∵若小华向后退0.5米到B处,这时他看自己的脚在镜中的像的俯角为30°,
∴AB=A1B1=0.5米,∠DB1B=30°,
∴tan30°=
| BD |
| BB 1 |
| BD |
| AB+ A1B1+AA1 |
| BD |
| 1+BD |
| ||
| 3 |
解得:BD=
| ||
| 2 |
| 1.73+1 |
| 2 |
答:小华的眼睛到地面的距离为1.4米.
点评:此题主要考查了解直角三角形中仰角与俯角问题以及平面镜成像的性质,得出AB=A1B1=0.5米,再利用锐角三角函数求出是解题关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
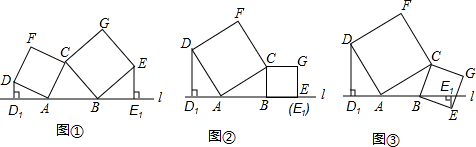
 (2012•盐城)如图是一个由3个相同的正方体组成的立体图形,则它的主视图为( )
(2012•盐城)如图是一个由3个相同的正方体组成的立体图形,则它的主视图为( )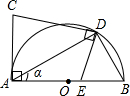 (2012•盐城)如图所示,AC⊥AB,AB=2
(2012•盐城)如图所示,AC⊥AB,AB=2
 (2012•盐城)如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是
(2012•盐城)如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 (2012•盐城)如图,在△ABC中,D、E分别是边AB、AC的中点,∠B=50°.先将△ADE沿DE折叠,点A落在三角形所在平面内的点为A1,则∠BDA1的度数为
(2012•盐城)如图,在△ABC中,D、E分别是边AB、AC的中点,∠B=50°.先将△ADE沿DE折叠,点A落在三角形所在平面内的点为A1,则∠BDA1的度数为