题目内容
已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论![]() 取什么实数值,该方程总有两个不相等的实数根;
取什么实数值,该方程总有两个不相等的实数根;
(2)当![]() 的斜边
的斜边![]() ,且两条直角边的长
,且两条直角边的长![]() 和
和![]() 恰好是这个方程的两个根时,求
恰好是这个方程的两个根时,求![]() 的值.
的值.
(1)证明:
![]() ,
,
因为无论![]() 取什么实数值,总有
取什么实数值,总有![]() ,即
,即![]() ,
,
所以无论![]() 取什么实数值,该方程总有两个不相等的实数根.
取什么实数值,该方程总有两个不相等的实数根.
(2)由一元二次方程根与系数的关系,得![]() ,
,
又在![]() 中,根据勾股定理
中,根据勾股定理![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]() ,
,
整理后,得![]() ,解这个方程,得
,解这个方程,得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,不符合题意,舍去,
,不符合题意,舍去,
当![]() 时,
时,![]() ,符合题意,故
,符合题意,故![]() .
.

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程  的一元二次方程
的一元二次方程 的两个整数根恰好比方程
的两个整数根恰好比方程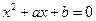 的两个根都大1,求
的两个根都大1,求 的值.
的值.  的一元二次方程x2+2x+m=0.
的一元二次方程x2+2x+m=0. 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根. 的取值范围;
的取值范围;