Question

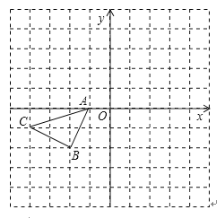
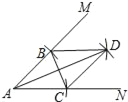
【题目】对于平面直角坐标系中的点，给出如下定义：若存在点（为正数），称点为点的等距点.例如：如图，对于点，存在点，点，则点分别为点的等距点.

（1）若点的坐标是，写出当时，点在第一象限的等距点坐标；

（2）若点的等距点的坐标是，求当点的横、纵坐标相同时的坐标；

（3）是否存在适当的值，当将某个点的所有等距点用线段依次连接起来所得到的图形周长不大于，求的取值范围.

Answer 1

【答案】（1）的等距点为；（2）点点坐标为；（3）.

【解析】

（1）根据等距点的定义可作判断；
（2）设点的坐标为，根据等距点的定义分两种情况列方程即可解答；
（3）根据题意画出图形可知．所有等距点用线段依次连接起来所得到的图形是矩形，其边长为2a，周长为8a，依据题意可得不等式求出a的取值范围.

解：（1）∵点的坐标是，当时，

∴点的等距点有（4，5）；（-4，-3），（4，-3），（-4，5）

∴点在第一象限的等距点坐标为；

（2）设点的坐标为，

由题意得，，

∴或

∴解得，

∴点点坐标为；

（3）由题意得，∴，

∴

∴的取值范围：.