题目内容
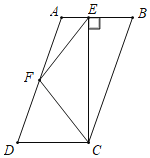
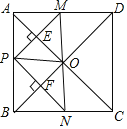
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点.动点
中点.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,点
运动,点![]() 关于点
关于点![]() 对称点为点
对称点为点![]() ,以
,以![]() 为边向上作正方形
为边向上作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
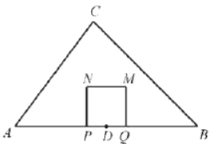
(1)当![]() _______秒时,点
_______秒时,点![]() 落在
落在![]() 边上.
边上.
(2)设正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() ,当点
,当点![]() 在
在![]() 内部时,求
内部时,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当正方形![]() 的对角线所在直线将
的对角线所在直线将![]() 的分为面积相等的两部分时,直接写出
的分为面积相等的两部分时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)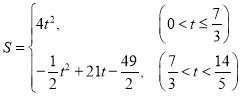 ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)如下图,根据![]() ,可得出PN与AP的关系,从而求出t的值;
,可得出PN与AP的关系,从而求出t的值;
(2)如下图,存在2种情况,一种是点M在△ABC内,另一种是点M在△ABC外部,分别根据正方形和三角形求面积的公式可求解;
(3)如下图,存在2种情况,一种是PM所在的直线将△ABC的面积平分,另一种是QN所在的直线将△ABC的面积平分.
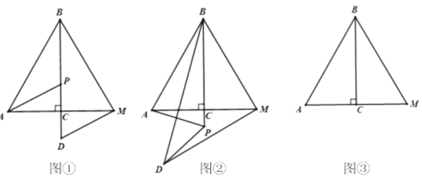
(1)如图1,点N在AC上
图1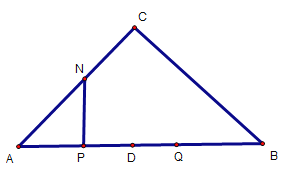
由题意可知:PD=DQ=t,AP=7-t
∴PN=PQ=2t
∵![]()
∴![]() ,即
,即![]()
解得:t=![]()
(2)①如图2,
图2
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,即
,即![]()
解得![]() ,
,
故当![]() ≤
≤![]() 时,
时,![]() ;
;
②如图3,
图3
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
则![]()
![]() ;
;
综上,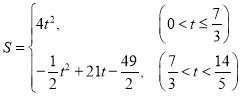 .
.
(3)如下图,过点C作AB的垂线,交AB于点G
图4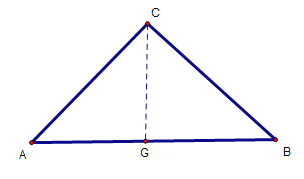
∵![]()
∴设CG=4x,则AG=3x
∵∠B=45°
∴△CBG是等腰直角三角形
∴GB=GC=4x
∵AB=14
∴3x+4x=14,解得:x=2
∴![]()
∴![]()
情况一:PM所在的直线平分△ABC的面积,如下图,PM与BC交于点E
图5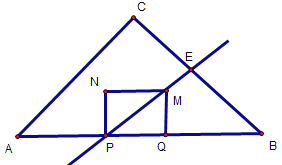
则![]()
∵四边形PQMN是正方形,∴∠EPB=45°
∵∠B=45°
∴△PBE是等腰直角三角形
∵![]()
∴PE=PB=![]()
∴PB=![]()
∵PB=AB-PA=14-(7-t)=7+t
∴7+t=![]()
t=![]()
情况二:如下图,QN所在线段平分△ABC的面积,QF交AC于点F,过点F作AB的垂线,交AB于点H
图6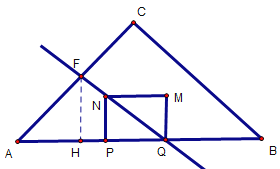
同理,![]()
∵四边形PQMN是正方形,∴∠EQH=45°
∴△FHQ是等腰直角三角形
∵![]()
∴设FH=4y,则AH=3y,HQ=FH=4y,∴AQ=7y
∴![]() ,解得:y=
,解得:y=![]()
∵AQ=AB-QB=14-(7-t)=7+t
∴7+t=7![]()
解得:t=7![]()
∴综上得:![]() 的值为
的值为![]() 或
或![]() .
.