题目内容
 如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F的距离,只需要测出线段________的长度.理由是依据________可以证明________,从而由全等三角形对应边相等得出.
如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F的距离,只需要测出线段________的长度.理由是依据________可以证明________,从而由全等三角形对应边相等得出.
EM 全等三角形的对应边相等 △BEM≌△CFM
分析:先根据SAS判定△BEM≌△CFM,从而得出CF=BE,即测量BE之间的距离相当于测量CF之间的距离.
解答:要想知道M与F的距离,只需要测出线段EM的长度.
理由是依据全等三角形的对应边相等可以证明△BEM≌△CFM,从而由全等三角形对应边相等得出.
证明:连接EF
∵AB∥CD,(已知)
∴∠B=∠C(两线平行内错角相等).
∵M是BC中点
∴BM=CM,
∵在△BEM和△CFM中,

∴△BEM≌△CFM(SAS).
∴CF=BE(对应边相等).
故答案为:EM,全等三角形的对应边相等,△BEM≌△CFM.
点评:本题考查了全等三角形的应用;关键是要把题目的问题转化为证明对应边相等.
分析:先根据SAS判定△BEM≌△CFM,从而得出CF=BE,即测量BE之间的距离相当于测量CF之间的距离.
解答:要想知道M与F的距离,只需要测出线段EM的长度.
理由是依据全等三角形的对应边相等可以证明△BEM≌△CFM,从而由全等三角形对应边相等得出.
证明:连接EF
∵AB∥CD,(已知)
∴∠B=∠C(两线平行内错角相等).
∵M是BC中点
∴BM=CM,
∵在△BEM和△CFM中,

∴△BEM≌△CFM(SAS).
∴CF=BE(对应边相等).
故答案为:EM,全等三角形的对应边相等,△BEM≌△CFM.
点评:本题考查了全等三角形的应用;关键是要把题目的问题转化为证明对应边相等.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
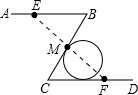 如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F的距离,只需要测出线段
如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F的距离,只需要测出线段 在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.
在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.
