题目内容
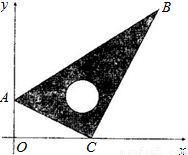
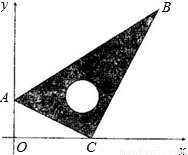
如图,将一块含30°角的学生用三角尺放在平面直角坐标系中,使顶点A,C分别放置在y轴,x轴上,已知AC=2,∠ACO=∠ABC=30°.(1)求点A,B,C的坐标;
(2)求经过A,B两点的直线的解析式.
【答案】分析:(1)在Rt△AOC中,利用“30°所对的直角边是斜边的一半”、勾股定理分别求得OA、OC的长度,从而求得点A、C的坐标;然后在Rt△ABC中,根据锐角三角函数求得BC=2 ;作BD⊥x轴交x轴于点D,易得CD=
;作BD⊥x轴交x轴于点D,易得CD= ,BD=3,从而求得点B的坐标;
,BD=3,从而求得点B的坐标;
(2)设直线AB:y=kx+b(k≠0).利用待定系数法求得一次函数的解析式.
解答: 解:(1)在Rt△AOC中,∠ACO=30°,AC=2,
解:(1)在Rt△AOC中,∠ACO=30°,AC=2,
∴AO= =1,CO=
=1,CO= ,
,
∴A(0,1),C( ,0).
,0).
在Rt△ABC中,∠ABC=30°,
∴ .
.
作BD⊥x轴交x轴于D,易得CD= ,BD=3,
,BD=3,
∴B( ,3);(3分)
,3);(3分)
(注:每个点的坐标各1分)
(2)设直线AB:y=kx+b(k≠0).
把A(0,1),B( ,3)代入,
,3)代入,
得 ,(4分)
,(4分)
解得: ,b=1(15分)
,b=1(15分)
∴直线AB的解析式为 .(6分)
.(6分)
点评:本题考查了一次函数综合题.在求点B的坐标时,通过作辅助线BD⊥x轴于D,然后在直角三角形BCD中求得点B的纵坐标,即BD的长度.
 ;作BD⊥x轴交x轴于点D,易得CD=
;作BD⊥x轴交x轴于点D,易得CD= ,BD=3,从而求得点B的坐标;
,BD=3,从而求得点B的坐标;(2)设直线AB:y=kx+b(k≠0).利用待定系数法求得一次函数的解析式.
解答:
 解:(1)在Rt△AOC中,∠ACO=30°,AC=2,
解:(1)在Rt△AOC中,∠ACO=30°,AC=2,∴AO=
 =1,CO=
=1,CO= ,
,∴A(0,1),C(
 ,0).
,0).在Rt△ABC中,∠ABC=30°,
∴
 .
.作BD⊥x轴交x轴于D,易得CD=
 ,BD=3,
,BD=3,∴B(
 ,3);(3分)
,3);(3分)(注:每个点的坐标各1分)
(2)设直线AB:y=kx+b(k≠0).
把A(0,1),B(
 ,3)代入,
,3)代入,得
 ,(4分)
,(4分)解得:
 ,b=1(15分)
,b=1(15分)∴直线AB的解析式为
 .(6分)
.(6分)点评:本题考查了一次函数综合题.在求点B的坐标时,通过作辅助线BD⊥x轴于D,然后在直角三角形BCD中求得点B的纵坐标,即BD的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
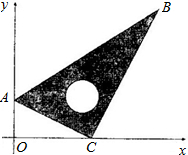 y轴,x轴上,已知AC=2,∠ACO=∠ABC=30°.
y轴,x轴上,已知AC=2,∠ACO=∠ABC=30°. (2013•沙湾区模拟)如图,将一块含30°的三角板叠放在直尺上.若∠1=40°,则∠2=( )
(2013•沙湾区模拟)如图,将一块含30°的三角板叠放在直尺上.若∠1=40°,则∠2=( ) 如图,将一块含30°角的学生用三角板放在平面直角坐标系中,使顶点A、B分别放置在y轴、x轴上,已知AB=2,∠ABO=∠ACB=30°.
如图,将一块含30°角的学生用三角板放在平面直角坐标系中,使顶点A、B分别放置在y轴、x轴上,已知AB=2,∠ABO=∠ACB=30°.