题目内容
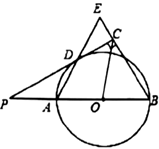
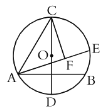
【题目】如图，在半径为4的
中，
为直径，弦
且过半径
的中点，
为上一动点，
于点
，即点在以
为直径的圆上，当从点
出发顺时针运动到点
时，点所经过的路径长为（ ）
A.
B.
C.
D.
【答案】C
【解析】
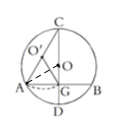
先找到当E与B、D重合时相应的F点
、
，因为
在以
为直径的圆上，所以劣弧
即为点所经过的路径，连AO，由
，得
，依据同弧所对的圆心角是圆周角的两倍，得到
，
，运用锐角三角函数求出，依据有一个角为60度的等腰三角形是等边三角形，可得
是等边三角形，从而
，最后用弧长公式计算即可.
解：∵
为直径，
∴
于点，
如图，取的中点为
，
∵当E与B重合时，
于点，当E与D重合时，
于点，
∴劣弧即为点所经过的路径，
连AO，
∵,
∴
∴，
，
∴
，，
∵，
，
∴是等边三角形，,
∴
=
=
，
故选：C.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
