题目内容
如图，已知在⊙O中，点A，B，C均在圆上，∠AOB=80°，则∠ACB等于
- A.130°
- B.140°
- C.145°
- D.150°
B
分析：设点E是优弧AB上的一点，连接EA，EB，根据同弧所对的圆周角是圆心角的一半可求得∠E的度数，再根据圆内接四边形的对角互补即可得到∠ACB的度数．
解答：
解：设点E是优弧AB上的一点，连接EA，EB
∵∠AOB=80°
∴∠E=
∠AOB=40°
∴∠ACB=180°-∠E=140°．
故选：B．
点评：本题主要考查了利用了圆周角定理，关键是掌握圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
分析：设点E是优弧AB上的一点，连接EA，EB，根据同弧所对的圆周角是圆心角的一半可求得∠E的度数，再根据圆内接四边形的对角互补即可得到∠ACB的度数．
解答：
解：设点E是优弧AB上的一点，连接EA，EB∵∠AOB=80°
∴∠E=
∠AOB=40°∴∠ACB=180°-∠E=140°．
故选：B．
点评：本题主要考查了利用了圆周角定理，关键是掌握圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
20、如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．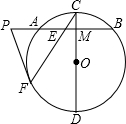
作⊙O的切线交BA的延长线于点P．
（2011•普宁市一模）如图，已知在?ABCD中，E、F是对角线BD延长线上的两点，且∠BCE=∠DAF，求证：△ECD≌△FAB．
如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠A的度数．