题目内容
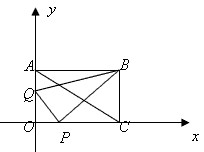
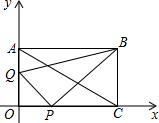 己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
| ||
| 3 |
(1)求线段AC的长和∠ACO的度数;
(2)动点P从点C开始在线段CO上以每秒
| 3 |
①设△BPQ的面积为S,求S与t之间的函数关系式,并求出当t为何值时,S有最小值;
②是否存在这样的时刻t,使得△OPQ与△BCP相似,并说明理由;
(3)在坐标平面内存在这样的点M,使得△MAC为等腰三角形且底角为30°,写出所有符合要求的点M的坐标.
分析:(1)根据直线AC的解析式可以求出直线与对称轴的交点坐标,进而求出OA、OC的长度,根据勾股定理就可以求出AC的长度,根据三角函数可以求出∠ACO的度数.
(2)①S△PBQ=S-S△POQ-S△PBC,而△PQO与△PBC的面积可以用时间t表示出来,就可以求出S与t之间的函数关系式.
②△OPQ与△BCP相似,应分△OPQ∽△CBP与△OPQ∽△CPB两种情况进行讨论.根据对应边的比相等,就可以求出函数的解析式.
(3)△MAC为等腰三角形且底角为30°,应分AC是底边与腰两种情况进行讨论.
(2)①S△PBQ=S-S△POQ-S△PBC,而△PQO与△PBC的面积可以用时间t表示出来,就可以求出S与t之间的函数关系式.
②△OPQ与△BCP相似,应分△OPQ∽△CBP与△OPQ∽△CPB两种情况进行讨论.根据对应边的比相等,就可以求出函数的解析式.
(3)△MAC为等腰三角形且底角为30°,应分AC是底边与腰两种情况进行讨论.
解答:解:(1)令x=0得y=-
×0+1=1
∴A点坐标为(0,1)
令y=0得0=-
×x+1=1
∴x=
C点坐标为(
,0)
∴AC=
=2
在Rt△AOC中,
∵tan∠ACO=
=
=
∴∠ACO=30°
(2)P、Q两点同时开始移动t秒时
①∵OQ=t,PC=
t
∴S△POQ=
×|OP|×|OQ|=
(1-t)t
S△PBC=
×|CP|×|BC|=
t×1
∵S△PBQ=S-S△POQ-S△PBC
∴S△PBQ=
(t-
)2+

∴当t=
时,S△PBQ最小值为
.
②i假设存在△OPQ∽△CBP
∴
=
=
∴t1=0(舍去),t2=
ii△OPQ∽△CPB
∴
=
=
∴t3=
,t4=
(舍去);
(3)M1(
,0),M2(
,1),M3(
,-2),M4(2
,1),M5(0,3),M6(-
,0).
| ||
| 3 |
∴A点坐标为(0,1)
令y=0得0=-
| ||
| 3 |
∴x=
| 3 |
| 3 |
∴AC=
| OA2+OC2 |
在Rt△AOC中,
∵tan∠ACO=
| OA |
| OC |
| 1 | ||
|
| ||
| 3 |
∴∠ACO=30°
(2)P、Q两点同时开始移动t秒时
①∵OQ=t,PC=
| 3 |
∴S△POQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∵S△PBQ=S-S△POQ-S△PBC
∴S△PBQ=
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |

∴当t=
| 1 |
| 2 |
3
| ||
| 8 |
②i假设存在△OPQ∽△CBP
∴
| OP |
| BC |
| OQ |
| PC |
| ||
| 1 |
| t | ||
|
∴t1=0(舍去),t2=
| 2 |
| 3 |
ii△OPQ∽△CPB
∴
| OP |
| PC |
| OQ |
| BC |
| ||
|
| t |
| 1 |
∴t3=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
(3)M1(
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查了三角函数的定义,求不规则图形的面积可以转化为一些规则图形的面积的和或差的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=- +1.
+1. 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒. +1.
+1. 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
 x+1 。
x+1 。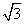 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。