题目内容
己知，如图在直角坐标系中，矩形OABC的对角线AC所在直线的解析式为y= -
x+1 。
（1）求线段AC的长和∠ACO的度数。
（2）动点P从点C开始在线段CO上以每秒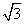
个单位长度的速度向点O移动，动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动，（P、Q两点同时开始移动）设P、Q移动的时间为t秒。
①设△BPQ的面积为S，求S与t之间的函数关系式，并求出当t为何值时，S有最小值。
②是否存在这样的时刻t，使得△OPQ与△BCP相似，并说明理由？
（3）在坐标平面内存在这样的点M，使得△MAC 为等腰三角形且底角为30°，写出所有符合要求的点M的坐标。
x+1 。（1）求线段AC的长和∠ACO的度数。
（2）动点P从点C开始在线段CO上以每秒
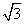个单位长度的速度向点O移动，动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动，（P、Q两点同时开始移动）设P、Q移动的时间为t秒。①设△BPQ的面积为S，求S与t之间的函数关系式，并求出当t为何值时，S有最小值。
②是否存在这样的时刻t，使得△OPQ与△BCP相似，并说明理由？
（3）在坐标平面内存在这样的点M，使得△MAC 为等腰三角形且底角为30°，写出所有符合要求的点M的坐标。
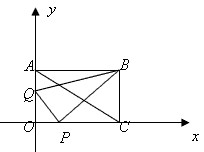
解：（1）令
得
∴A点坐标为（0，1）
令
得 
∴
C点坐标为（
，0）
∴
在
中， ∵
∴
（2）P、Q两点同时开始移动t秒时
① ∵
t
∴
t×1
∵
∴
∴当
时，
最大为
②ⅰ：假设存在
∽
∴
即 
∴
ⅱ：
∽
∴
即
∴
，
（3）
，
，
，
，
，
得 ∴A点坐标为（0，1）令
得 ∴
C点坐标为（，0）∴
在
中， ∵ ∴（2）P、Q两点同时开始移动t秒时
① ∵
t∴
t×1∵
∴
∴当
时，最大为②ⅰ：假设存在
∽ ∴ 即 ∴ⅱ：
∽ ∴ 即 ∴，（3）
，，，，，
练习册系列答案
阳光课堂课时作业系列答案
相关题目
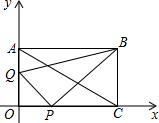己知，如图在直角坐标系中，矩形OABC的对角线AC所在直线的解析式为y=-
己知，如图在直角坐标系中，矩形OABC的对角线AC所在直线的解析式为y=-
+1．
个单位长度的速度向点O移动，动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动，（P、Q两点同时开始移动）设P、Q移动的时间为t秒．
+1．
个单位长度的速度向点O移动，动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动，（P、Q两点同时开始移动）设P、Q移动的时间为t秒．
,
) B(
,
) D.(
)