题目内容
12. 如图,在△ABC中,∠A=30°,∠B=45°,AC=$2\sqrt{3}$,则AB的长为( )
如图,在△ABC中,∠A=30°,∠B=45°,AC=$2\sqrt{3}$,则AB的长为( )| A. | 3+$\sqrt{3}$ | B. | 2+2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 6 |
分析 过C作CD⊥AB于D,求出∠BCD=∠B,推出BD=CD,根据含30度角的直角三角形求出CD,根据勾股定理求出AD,相加即可求出答案.
解答 解:过C作CD⊥AB于D,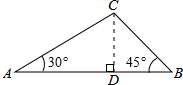
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2$\sqrt{3}$,
∴CD=$\sqrt{3}$,
∴BD=CD=$\sqrt{3}$,
由勾股定理得:AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=3,
∴AB=AD+BD=3+$\sqrt{3}$.
故选A.
点评 本题考查了勾股定理,等腰三角形的性质和判定,含30度角的直角三角形性质等知识点的应用,关键是构造直角三角形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a100的值为( )
| A. | -49 | B. | -50 | C. | -99 | D. | -100 |
3.下列一次函数中,y的值随着x值的增大而减小的有( )
①y=10x-9;
②y=-0.3x+2;
③y=$\sqrt{5}$x+4;
④y=($\sqrt{2}$-$\sqrt{3}$)x;
⑤y=7-$\frac{1}{2}$x;
⑥y=8+($\sqrt{5}$-2)x.
①y=10x-9;
②y=-0.3x+2;
③y=$\sqrt{5}$x+4;
④y=($\sqrt{2}$-$\sqrt{3}$)x;
⑤y=7-$\frac{1}{2}$x;
⑥y=8+($\sqrt{5}$-2)x.
| A. | ①③⑥ | B. | ②⑤⑥ | C. | ④⑤⑥ | D. | ②④⑤ |
20.下列等式从左到右的变形,属于因式分解的是( )
| A. | 6a3b=3a2•2ab | B. | t2-3t-10=(t+2)(t-5) | ||
| C. | a2-b2+1=(a+b)(a-b)+1 | D. | (x+y)2=x2+2xy+y2 |
7.若4x2+mxy+16y2是一个完全平方式,则m的值为( )
| A. | 8 | B. | 16 | C. | ±16 | D. | ±8 |
2. 在图中的数轴上,表示-$\frac{1}{3}$的是( )
在图中的数轴上,表示-$\frac{1}{3}$的是( )
 在图中的数轴上,表示-$\frac{1}{3}$的是( )
在图中的数轴上,表示-$\frac{1}{3}$的是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |