Question

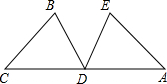（1）如图，已知∠C=∠A，∠B=∠E，点D为CA的中点，说明下列判断成立的理由．
（i）△BDC≌△EDA；（ii）CB=AE．

（2）如图，已知∠BAD=∠CAE，AB=AD，AC=AE，
则：（1）△ABC≌△ADE，（2）∠B=∠D，请说明理由．
解：∵∠BAD=______（已知）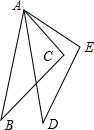
∴∠BAD+∠DAC=______+______
即______
在△ABC与△ADE中，∴______（______）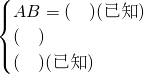
∴∠B=∠D（______）

Answer 1

（1）解：∵点D为CA的中点，
∴CD=AD．
在与△BDC与△EDA中，

∴△BDC≌△EDA（AAS）．

（2）∵△BDC≌△EDA，
∴CB=AE．
分析：由已知条件用“AAS”可判定△BDC≌△EDA，利用全等的性质：对应边相等可得：CB=AE．
点评：本题考查了全等三角形的判断和性质，常用的判断方法为：SAS，SSS，AAS，ASA．常用到的性质是：对应角相等，对应边相等．在证明中还要注意图形中隐藏条件的挖掘如：本题中的公共角∠DAC．