题目内容
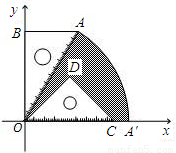
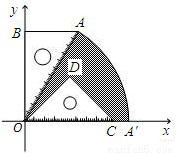
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
(1)若双曲线的一个分支恰好经过点A,求双曲线的解析式;
(2)若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A',试求图中阴影部分的面积(结果保留π).
(1)若双曲线的一个分支恰好经过点A,求双曲线的解析式;
(2)若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A',试求图中阴影部分的面积(结果保留π).

解:(1 )在Rt △OBA 中,∠AOB=30 °,AB=3 ,cot ∠AOB= ,
,
∴OB=ABcot30°=3 ,∴点A(3,3
,∴点A(3,3 ).
).
设双曲线的解析式为y= (k≠0).∴3
(k≠0).∴3 =
= ,k=9
,k=9 .
.
则双曲线的解析式为y= .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,sin∠AOB= ,sin30°=
,sin30°= ,
,
∴OA=6.
由题意得:∠AOC=60°,
S扇形AOA ′= .
.
在Rt△OCD中,∠DOC=45°,OC=OB=3 ,
,
∴OD=OCcos45°=3
 .
.
∴S△ODC= .
.
∴S阴影=S扇形AOA′﹣S△ODC=6π﹣ .
.

 ,
,∴OB=ABcot30°=3
 ,∴点A(3,3
,∴点A(3,3 ).
).设双曲线的解析式为y=
 (k≠0).∴3
(k≠0).∴3 =
= ,k=9
,k=9 .
.则双曲线的解析式为y=
 .
.(2)在Rt△OBA中,∠AOB=30°,AB=3,sin∠AOB=
 ,sin30°=
,sin30°= ,
,∴OA=6.
由题意得:∠AOC=60°,
S扇形AOA ′=
 .
.在Rt△OCD中,∠DOC=45°,OC=OB=3
 ,
,∴OD=OCcos45°=3

 .
.∴S△ODC=
 .
.∴S阴影=S扇形AOA′﹣S△ODC=6π﹣
 .
.


练习册系列答案
相关题目
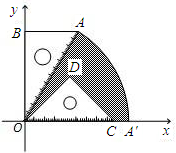 已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.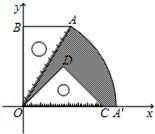 已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,
已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,