Question

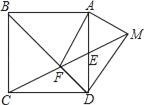
【题目】如图，在平面直角坐标系中，点的坐标分别是，，若二次函数的图象过两点，且该函数图象的顶点为，其中，是整数，且，，则的值为__________．

Answer 1

【答案】，

【解析】

先将A，B两点的坐标代入，消去c可得出b=1-7a，c=10a，得出xM=-=，yM=.方法一：分以下两种情况：①a＞0，画出示意图，可得出yM=0,1或2，进而求出a的值；②a＜0时，根据示意图可得，yM=5，6或7，进而求出a的值；方法二：根据题意可知或7①，或7②，由①求出a的值，代入②中验证取舍从而可得出a的值．

解：将A，B两点的坐标代入得，

，

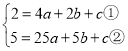②-①得，3=21a+3b，

∴b=1-7a，c=10a．

∴原解析式可以化为：y=ax2+(1-7a)x+10a．

∴xM=-=，yM=,

方法一：

①当a＞0时，开口向上，∵二次函数经过A,B两点，且顶点中，x，y均为整数，且，，画出示意图如图①，可得0≤yM≤2，

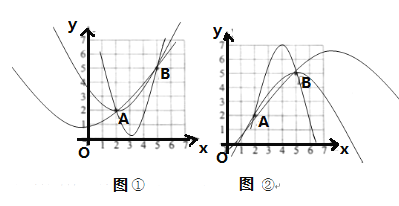
∴yM=0,1或2，

当yM=0时，解得a=,不满足xM为整数的条件，舍去；

当yM=1时，解得a=1(a=不符合条件，舍去)；

当yM=2时，解得a=,符合条件．

②a＜0时，开口向下，画出示意图如图②，根据题中条件可得，5≤yM≤7，

只有当yM=5，a=-时，当yM=6，a=-1时符合条件．

综上所述，a的值为，．

方法二：

根据题意可得或7；或7③，

∴当时，解得a=，不符合③，舍去；

当时，解得a=，不符合③，舍去；

当时，解得a=，符合③中条件；

当时，解得a=1，符合③中条件；

当时，解得a=-1，符合③中条件；

当时，解得a=-，符合③中条件；

当时，解得a=-，不符合③舍去；

当时，解得a=-，不符合③舍去；

综上可知a的值为：，．

故答案为：，