题目内容
如图,在□ OABC中,点A在x轴上,∠AOC=60o,0C=4cm.OA=8cm.动点P从点0出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以
acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.
设运动时间为t秒.
(1)填空:点C的坐标是(______,______),对角线OB的长度是_______cm;
(2)当a=1时,设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
(3)当点P在OA边上,点Q在CB边上时,线段PQ与对角线OB交于点M.若以O、M、P
为顶点的三角形与△OAB相似,求a与t的函数关系式,并直接写出t的取值范围.

解:(1)C(2,2![]() ),OB=4
),OB=4![]() cm.……………………4分
cm.……………………4分
(2)①当0<t≤4时,
过点Q作QD⊥x轴于点D(如图1),则QD=![]() t.
t.
∴S=![]() OP·QD=
OP·QD=![]() t2. ………………………5分
t2. ………………………5分
②当4≤t≤8时,
作QE⊥x轴于点E(如图2),则QE=2![]() .
.
∴S =![]() DP·QE=
DP·QE=![]() t. ……………………6分
t. ……………………6分



③当8≤t<12时,
解法一:延长QP交x轴于点F,过点P作PH⊥AF于点H(如图3).
易证△PBQ与△PAF均为等边三角形,
∴OF=OA+AP=t,AP=t-8.
∴PH=![]() (t-8). …………………………………7分
(t-8). …………………………………7分
∴S=S△OQF-S△OPF
=![]() t·2
t·2![]() -
-![]() t·
t·![]() (t-8)
(t-8)
=-![]() t2+3
t2+3![]() t. …………………………………………………………………8分
t. …………………………………………………………………8分
当t=8时,S最大. …………………………………………………………………9分
解法二:过点P作PH⊥x轴于点H(如图3).
易证△PBQ为等边三角形.
∵AP=t-8.
∴PH=![]() (t-8). ………………………………………………………………………7分
(t-8). ………………………………………………………………………7分
∴S=S梯形OABQ-S△PBQ- S△OAP
=![]() (20-t)-
(20-t)- ![]() (12-t)2-2
(12-t)2-2![]() (t-8).
(t-8).
=-![]() t2+3
t2+3![]() t. ……………………………………………………………………8分
t. ……………………………………………………………………8分
当t=8时,S最大. ……………………………………………………………………![]() 9分
9分
(其它解法酌情给分,如S=S□OABC-S△OAP- S△OCQ - S△PBQ )
 (3)①当△OPM~△OAB时(如图4),则PQ∥AB.
(3)①当△OPM~△OAB时(如图4),则PQ∥AB.
∴CQ=OP.
∴at-4=t,a=1+![]() . ………………………………10分
. ………………………………10分
t的取值范围是0<t≤8. …………………………11分
 ②当△OPM~△OBA时(如图5),
②当△OPM~△OBA时(如图5),
则![]() ,
,
∴![]() ,
,
∴OM=![]() . ………………………………………………………………………12分
. ………………………………………………………………………12分
又∵QB∥OP,
∴△BQM~△OPM,
∴![]() ,
,
∴ ,
,
整理得t-at=2,∴a=1-![]() . …………………………………………………………13分
. …………………………………………………………13分
t的取值范围是6≤t≤8.
综上所述:a=1+![]() (0<t≤8)或a=1-
(0<t≤8)或a=1-![]() (6≤t≤8). …………………………………14分
(6≤t≤8). …………………………………14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案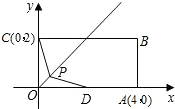 出此时点P的坐标和△PDE的周长.
出此时点P的坐标和△PDE的周长.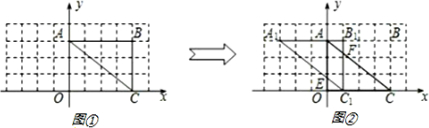
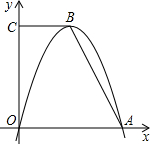 如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.
如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积. (2012•莆田质检)如图,在矩形OABC中,OA、OC两边分别在x轴、y轴的正半轴上,OA=3,OC=2,过OA边上的D点,沿着BD翻折△ABD,点A恰好落在BC边上的点E处,反比例函数
(2012•莆田质检)如图,在矩形OABC中,OA、OC两边分别在x轴、y轴的正半轴上,OA=3,OC=2,过OA边上的D点,沿着BD翻折△ABD,点A恰好落在BC边上的点E处,反比例函数 (2013•桐乡市一模)如图,在正方形OABC中,已知A(-2,0),C(0,2),将正方形OABC向右平移3个单位长度,得到正方形O′A′B′C′,则点B的对应点B′的坐标是
(2013•桐乡市一模)如图,在正方形OABC中,已知A(-2,0),C(0,2),将正方形OABC向右平移3个单位长度,得到正方形O′A′B′C′,则点B的对应点B′的坐标是