题目内容
对于正数x规定f(x)= ,例如f(3)=
,例如f(3)=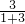 =
= f(
f( )=
)=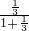 =
= 则f(
则f( )+f(
)+f( )+…+f(1)+f(2010)=
)+…+f(1)+f(2010)=
- A.2010
- B.1005
- C.2009.5
- D.2010.5
C
分析:通过计算f(1)+f(1)=1,f(2)+f( )=1,f(3)+f(
)=1,f(3)+f( )=1,…可以推出则f(
)=1,…可以推出则f( )+f(
)+f( )+…+f(1)+f(2010)结果.
)+…+f(1)+f(2010)结果.
解答:因为f(1)=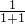 =
= ,f(1)+f(1)=1,
,f(1)+f(1)=1,
f(2)=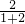 =
= ,f(
,f( )=
)= =
= ,f(2)+f(
,f(2)+f( )=1,
)=1,
f(3)=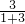 =
= ,f(
,f( )=
)=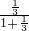 =
= ,f(3)+f(
,f(3)+f( )=1,
)=1,
…
f(2010)= =
= ,f(
,f( )=
)= =
= ,f(2010)+f(
,f(2010)+f( )=1,
)=1,
所以f( )+f(
)+f( )+…+f(1)+f(2010)=2010-
)+…+f(1)+f(2010)=2010- =2009.5.
=2009.5.
故选C.
点评:解决此题的关键是发现f(n)+f( )=1,问题容易解决.
)=1,问题容易解决.
分析:通过计算f(1)+f(1)=1,f(2)+f(
 )=1,f(3)+f(
)=1,f(3)+f( )=1,…可以推出则f(
)=1,…可以推出则f( )+f(
)+f( )+…+f(1)+f(2010)结果.
)+…+f(1)+f(2010)结果.解答:因为f(1)=
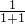 =
= ,f(1)+f(1)=1,
,f(1)+f(1)=1,f(2)=
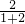 =
= ,f(
,f( )=
)= =
= ,f(2)+f(
,f(2)+f( )=1,
)=1,f(3)=
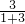 =
= ,f(
,f( )=
)=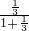 =
= ,f(3)+f(
,f(3)+f( )=1,
)=1,…
f(2010)=
 =
= ,f(
,f( )=
)= =
= ,f(2010)+f(
,f(2010)+f( )=1,
)=1,所以f(
 )+f(
)+f( )+…+f(1)+f(2010)=2010-
)+…+f(1)+f(2010)=2010- =2009.5.
=2009.5.故选C.
点评:解决此题的关键是发现f(n)+f(
 )=1,问题容易解决.
)=1,问题容易解决. 
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
对于正数x规定f(x)=
,例如f(3)=
=
f(
)=
=
则f(
)+f(
)+…+f(1)+f(2010)=( )
| x |
| 1+x |
| 3 |
| 1+3 |
| 3 |
| 4 |
| 1 |
| 3 |
| ||
1+
|
| 1 |
| 4 |
| 1 |
| 2010 |
| 1 |
| 2009 |
| A、2010 |
| B、1005 |
| C、2009.5 |
| D、2010.5 |
 ;
;  =
= .请你计算:
.请你计算: +
+ +
+ +…+
+…+ +f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)=______.
+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)=______. ,例如:f(3)=
,例如:f(3)= ;
;  =
= .请你计算:
.请你计算: +
+ +
+ +…+
+…+ +
+ +f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)= .
+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)= .