题目内容
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )

A.3 B.4 C.6 D.5
A【考点】角平分线的性质.
【专题】几何图形问题.
【分析】过点D作DF⊥AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再根据S△ABC=S△ABD+S△ACD列出方程求解即可.
【解答】解:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC=S△ABD+S△ACD,
∴ ×4×2+
×4×2+ ×AC×2=7,
×AC×2=7,
解得AC=3.
故选:A.

【点评】本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
 ,BC=2,则这个三角形是( )
,BC=2,则这个三角形是( )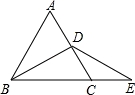

 ,结果是( )
,结果是( ) D.
D.
 ∠β,(不写作法,保留作图痕迹)
∠β,(不写作法,保留作图痕迹)