题目内容
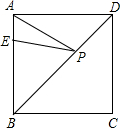如图，E是边长为4cm的正方形ABCD的边AB上一点，且AE=1cm，P为对角线BD上的任意一点，则AP+EP的最小值是分析：作E点关于直线BD的对称点E′，连接AE′，则线段AE′的长即为AP+EP的最小值，根据正方形的性质可知E′必在BC上，且BE=AB-AE-4-1=3，再在Rt△ABE′中利用勾股定理即可求出AE′的长．
解答：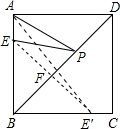
解：作E点关于直线BD的对称点E′，连接AE′，则线段AE′的长即为AP+EP的最小值，
∵四边形ABCD是正方形，
∴BD平分∠ABC，
∵EE′⊥BD，
∴E′在BC上，且BE′=BE=AB-AE=4-1=3，
在Rt△ABE′中，AE′=
=
=5．
故答案为：5．
解：作E点关于直线BD的对称点E′，连接AE′，则线段AE′的长即为AP+EP的最小值，∵四边形ABCD是正方形，
∴BD平分∠ABC，
∵EE′⊥BD，
∴E′在BC上，且BE′=BE=AB-AE=4-1=3，
在Rt△ABE′中，AE′=
| AB2+BE′2 |
| 42+32 |
故答案为：5．
点评：本题考查的是轴对称，最短路线问题，根据题意作出E关于BD的对称点是解答此题的关键．
练习册系列答案
相关题目
14、如图，O是边长为6的等边三角形ABC内的任意一点，且OD∥BC，交AB于点D，OF∥AB，交AC于F，OE∥AC，交BC于E．则OD+OE+OF的值（ ）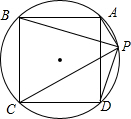
如图，⊙O是边长为1的正方形ABCD的外接圆，P为弧AD上的不同于A、D的任意一点，则PA2+PB2+PC2+PD2的值为（ ）
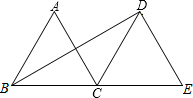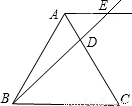
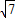
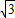
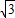
如图，△ABC是边长为
如图，⊙O是边长为1的正方形ABCD的外接圆，P为弧AD上的不同于A、D的任意一点，则PA2+PB2+PC2+PD2的值为（ ）