Question

【题目】如图，在等腰△ABC中，点D、E分别是边AB、AC上的两点（点D不与点A、 点B重合），且DE∥BC，以DE为一边，在四边形DBCE的内部作正方形DEFG，已知AB=AC=5，BC=6．

（1）试求△ABC的面积；

（2）当GF与BC重合时，求正方形DEFG的边长；

（3）若BG的长度等于正方形DEFG的边长，试求AD的长．

Answer 1

【答案】（1）12（2） （3）

【解析】试题分析：(1)作底边上的高,利用勾股定理求出高就可以求出面积.

(2)根据DE∥BC,得到△ADE∽△ABC,再根据相似三角形对应高的比等于相似比即可求出边DE的长度.

（3）设AD为y，作GH⊥BD，由△ADE∽△ABC，由△ADE∽△ABC，得，

由△BGH∽△ABM，得．

解：（1）作AM⊥BC交BC与M，

∵AB=AC，∴BE=EC=3，

在Rt△AMC中，由，可得AM=4，

∴．

（2）设正方形边长为x，AM交DE于点N，由题意，得△ADE∽△ABC，

∴，∴，

解得，∴正方形DEFG的边长为．

（3）设AD为y，作GH⊥BD，

由△ADE∽△ABC，得，即，解得，

由△BGH∽△ABM，得，即，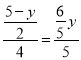

解之得，∴AD的长为．