题目内容
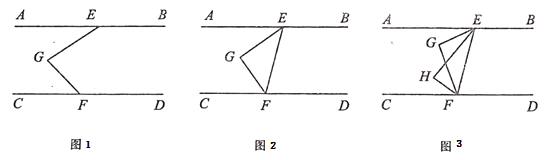
【题目】已知,点P是等边△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若∠APB=150°,PA=9,PB=12,求PC的长度.

【答案】(1)详见解析;(2)PC=15
【解析】
(1)利用旋转的性质找到证明△BAP≌△CAQ,,然后利用全等三角形的性质即可证明;
(2)利用等边三角形的性质和勾股定理解答即可.
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,
∴∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,BA=CA,∠BAP=∠CAQ,AP=AQ
∴△BAP≌△CAQ(SAS);
∴PB=QC;
(2)解:∵△APQ是等边三角形,
∴AP=PQ=9,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°-60°=90°,
∵PB=QC=12,
∴△PQC是直角三角形,
∴PC=![]() .
.

【题目】某中学1000名学生参加了“环保知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x<90 | b | c |
合计 | ■ | 1 |
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
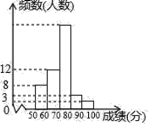
【题目】光明电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 2台 | 6台 | 1840元 |
第二周 | 5台 | 7台 | 2840 元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备再采购这两种型号的电风扇共40台,这40台电风扇全部售出后,若利润不低于2660元,求A种型号的电风扇至少要采购多少台?