Question

已知：如图1，△OAB是边长为2的等边三角形，OA在x轴上，点B在第一象限内；△OCA是一个等腰三角形，OC＝AC，顶点C在第四象限，∠C＝120°．现有两动点P、Q分别从A、O两点同时出发，点Q以每秒1个单位的速度沿OC向点C运动，点P以每秒3个单位的速度沿A→O→B运动，当其中一个点到达终点时，另一个点也随即停止．

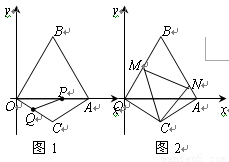
（1）求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系，并写出自变量t的取值范围；

（2）在OA上（点O、A除外）存在点D，使得△OCD为等腰三角形，请直接写出所有符合条件的点D的坐标；

（3）如图2，现有∠MCN＝60°，其两边分别与OB、AB交于点M、N，连接MN．将∠MCN绕着C点旋转（0°＜旋转角＜60°），使得M、N始终在边OB和边AB上．试判断在这一过程中，△BMN的周长是否发生变化？若没有变化，请求出其周长；若发生变化，请说明理由．

 

Answer 1

【答案】

（1）当时，，当时，（2）或  （3）的周长不发生变化，周长为4

【解析】（1）过点C作CD⊥OA于点D． ……………………………………1分

∵OC=AC，∠ACO=120°，∴∠AOC=∠OAC=30°．

      ∵，， ∴．

   在Rt中，  ………………………2分

 （1）当时，,,；

过点作于点．

     在Rt中，∵，∴，……………………3分

∴．

  即 ．……………………………………………………………4分

   （2）当时，

，．……………………………………………………5分

∵，，∴．

∴．

即．………………………………………………………………6分

故当时，，当时，

（2）或         ……………………………………………8分

（3）的周长不发生变化．

延长至点，使，连结．………………………………9分

∵，∴≌．

∴，  …………………………………………10分

       ∴．

        ∴． 又∵．

   ∴≌．∴   ……………………………………11分

∴．

∴的周长不变，其周长为4   ……………………………………12分

（1）分P点在AO、BO边两种情况进行讨论；

（2）分OD=OC、CD=CD两种情况进行讨论；

（3）利用等量代换得出三个边之和为一定值，说明的周长不变。