题目内容

10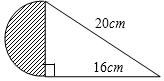．如图，如果半圆的直径恰为直角三角形的一条直角边，那么半圆的面积是（　　）
A．8π cm2B．12π cm2C．16π cm2D．18π cm2

分析 先根据已知条件利用勾股定理可得三角形的直角边（即半圆的直径），再得出半径的值，然后求出圆的面积即可得出答案．

解答 解：由勾股定理可得，三角形的直角边（即半圆的直径）为：$\sqrt{2{0}^{2}-1{6}^{2}}$=12，
所以半径r=6，
故S半圆=$\frac{1}{2}$πr2=18π，
故选：D．

点评 此题主要考查了学生对勾股定理和圆面积的理解和掌握，解决问题的关键是掌握半圆面积的算法，以及勾股定理的运用．

练习册系列答案
相关题目
20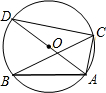．如图，△ABC内接于圆O，AD是圆O的直径，∠ABC=30°，则∠CAD的度数等于（　　）
A．45°B．50°C．55°D．60°
1．计算与解方程：
（1）（$\sqrt{3}$）0+（-2）2-（$\frac{1}{3}$）-2；         
（2）$\sqrt{（-3）^{2}}$-|2-$\sqrt{2}$|-$\root{3}{8}$
（3）（x+2）2-64=0；                  
（4）（x-3）3=-27．
18．计算：20160+（$\frac{1}{2}$）-1-$\sqrt{2}$sin45°+tan60°．
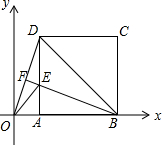5．如图，在平面直角坐标系中，边长为$\sqrt{2}$的正方形ABCD的顶点A，B在x轴上，连接OD、BD、△BOD的外心I在中线上，BF与AD交于点E，连接OE，若点M是直线BF上的一动点，且△BMD与△OED相似，则点M的坐标（1，$\sqrt{2}$-1）或（-$\sqrt{2}$，$\sqrt{2}$）．
15．将下列实数填在相应的集合中：
-7，0.32，$\frac{1}{7}$，$\sqrt{5}$，0，-$\sqrt{（-3）^2}$，0.7171171117…，0.3$\stackrel{•}{4}$，π，$\root{3}{9}$
（1）整数集合{-7，0，-$\sqrt{（-3）^2}$ …}   
（2）分数集合：{0.32，$\frac{1}{7}$，0.3$\stackrel{•}{4}$…}
（3）负实数集合：{-7，-$\sqrt{（-3）^2}$…}  
（4）无理数集合：{$\sqrt{5}$，0.7171171117…，π，$\root{3}{9}$…}．
2．下列各式，①-（-2）； ②-|-2|； ③-23； ④-（-2）2．计算结果为负数的个数有（　　）
A．4个B．3个C．2个D．1个
19．计算与化简
（1）-7+13-6+20         
（2）23×（-5）-（-3）÷$\frac{3}{128}$
（3）[-22-（5-6）3]÷$\frac{15}{4}$×$\frac{4}{3}$-|-2|
（4）-（2y-5）+（4+3y）         
（5）（8xy-x2+y2）-3（-x2+y2+5xy）
20．计算：
（1）-4÷$\frac{2}{3}$-（-$\frac{2}{3}$）×（-30）
（2）-40-28-（-19）+（-24）
（3）（4x2y-3xy2）-（1+4x2y-3xy2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网