题目内容
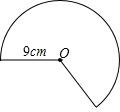（2013•泸州）如图，从半径为9cm的圆形纸片上剪去| 1 |
| 3 |
3
| 5 |
3
cm．| 5 |
分析：首先求得扇形的弧长，即圆锥的底面周长，则底面半径即可求得，然后利用勾股定理即可求得圆锥的高．
解答：解：圆心角是：360×（1-
）=240°，
则弧长是：
=12π（cm），
设圆锥的底面半径是r，则2πr=12π，
解得：r=6，
则圆锥的高是：
=3
（cm）．
故答案是：3
．
| 1 |
| 3 |
则弧长是：
| 240π×9 |
| 180 |
设圆锥的底面半径是r，则2πr=12π，
解得：r=6，
则圆锥的高是：
| 92-62 |
| 5 |
故答案是：3
| 5 |
点评：正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
（2013•泸州）如图所示为某几何体的示意图，则该几何体的主视图应为（ ）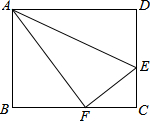
（2013•泸州）如图，点E是矩形ABCD的边CD上一点，把△ADE沿AE对折，点D的对称点F恰好落在BC上，已知折痕AE=10
（2013•泸州）如图，在等腰直角△ACB中，∠ACB=90°，O是斜边AB的中点，点D、E分别在直角边AC、BC上，且∠DOE=90°，DE交OC于点P．则下列结论：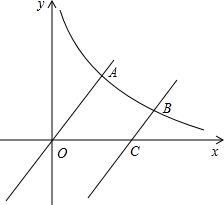
（2013•泸州）如图，已知函数y=
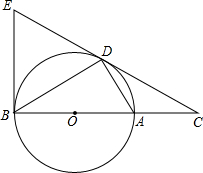（2013•泸州）如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．