题目内容
 (2013•泸州)如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
(2013•泸州)如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)图形中全等的三角形只有两对;
(2)△ABC的面积等于四边形CDOE的面积的2倍;
(3)CD+CE=
| 2 |
其中正确的结论有( )
分析:结论(1)错误.因为图中全等的三角形有3对;
结论(2)正确.由全等三角形的性质可以判断;
结论(3)正确.利用全等三角形和等腰直角三角形的性质可以判断.
结论(4)正确.利用相似三角形、全等三角形、等腰直角三角形和勾股定理进行判断.
结论(2)正确.由全等三角形的性质可以判断;
结论(3)正确.利用全等三角形和等腰直角三角形的性质可以判断.
结论(4)正确.利用相似三角形、全等三角形、等腰直角三角形和勾股定理进行判断.
解答:解:
结论(1)错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.
在△AOD与△COE中,
∴△AOD≌△COE(ASA).同理可证:△COD≌△BOE.
结论(2)正确.理由如下:
∵△AOD≌△COE,∴S△AOD=S△COE,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=
S△ABC,
即△ABC的面积等于四边形CDOE的面积的2倍.
结论(3)正确,理由如下:
∵△AOD≌△COE,∴CE=AD,
∴CD+CE=CD+AD=AC=
OA.
结论(4)正确,理由如下:
∵△AOD≌△COE,∴AD=CE;∵△COD≌△BOE,∴BE=CD.
在Rt△CDE中,由勾股定理得:CD2+CE2=DE2,∴AD2+BE2=DE2.
∵△AOD≌△COE,∴OD=OE,
又∵OD⊥OE,∴△DOE为等腰直角三角形,∴DE2=2OE2,∠DEO=45°.
∵∠DEO=∠OCE=45°,∠COE=∠COE,
∴△OEP∽△OCE,
∴
=
,即OP•OC=OE2.
∴DE2=2OE2=2OP•OC,
∴AD2+BE2=2OP•OC.
综上所述,正确的结论有3个,故选C.
结论(1)错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.
在△AOD与△COE中,
|
∴△AOD≌△COE(ASA).同理可证:△COD≌△BOE.

结论(2)正确.理由如下:
∵△AOD≌△COE,∴S△AOD=S△COE,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=
| 1 |
| 2 |
即△ABC的面积等于四边形CDOE的面积的2倍.
结论(3)正确,理由如下:
∵△AOD≌△COE,∴CE=AD,
∴CD+CE=CD+AD=AC=
| 2 |
结论(4)正确,理由如下:
∵△AOD≌△COE,∴AD=CE;∵△COD≌△BOE,∴BE=CD.
在Rt△CDE中,由勾股定理得:CD2+CE2=DE2,∴AD2+BE2=DE2.
∵△AOD≌△COE,∴OD=OE,
又∵OD⊥OE,∴△DOE为等腰直角三角形,∴DE2=2OE2,∠DEO=45°.
∵∠DEO=∠OCE=45°,∠COE=∠COE,
∴△OEP∽△OCE,
∴
| OE |
| OC |
| OP |
| OE |
∴DE2=2OE2=2OP•OC,
∴AD2+BE2=2OP•OC.
综上所述,正确的结论有3个,故选C.
点评:本题是几何综合题,考查了等腰直角三角形、全等三角形、相似三角形和勾股定理等重要几何知识点.难点在于结论(4)的判断,其中对于“OP•OC”线段乘积的形式,可以寻求相似三角形解决问题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 (2013•泸州)如图所示为某几何体的示意图,则该几何体的主视图应为( )
(2013•泸州)如图所示为某几何体的示意图,则该几何体的主视图应为( )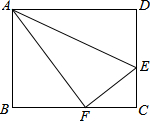 (2013•泸州)如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
(2013•泸州)如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10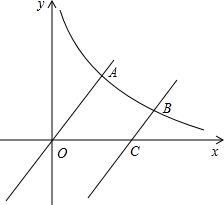 (2013•泸州)如图,已知函数y=
(2013•泸州)如图,已知函数y=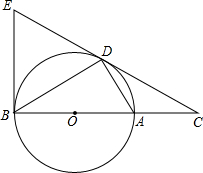 (2013•泸州)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(2013•泸州)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.