题目内容
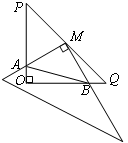
在Rt⊿POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与⊿POQ的两直角边分别交于点A、B,
(1)求证:MA=MB
(2)连接AB,探究:在旋转三角尺的过程中,⊿AOB的周长是否存在最小值,若存在,求出最小值,若不存在。请说明理由。

(1)证明:连接OM ∵ Rt⊿POQ中,OP=OQ =4,M是PQ的中点
∴OM=PM=![]() PQ=2
PQ=2![]()
∠POM=∠BOM=∠P=450 ∵∠PMA+∠AMO=∠OMB+∠AMO
 ∴∠PMA=∠OMB ⊿PMA≌⊿OMB ∴ MA=MB
∴∠PMA=∠OMB ⊿PMA≌⊿OMB ∴ MA=MB
(2)解:⊿AOB的周长存在最小值
理由是: ⊿PMA≌⊿OMB ∴ PA=OB
∴OA+OB=OA+PA=OP=4
令OA=x AB=y则y2=x2+(4-x)2=2x2-8x+16
=2(x-2)2+8≥8
当x=2时y2有最小值=8从而 y≥2![]()
故⊿AOB的周长存在最小值,其最小值是4+2![]() 新 课标 第 一网
新 课标 第 一网

练习册系列答案
相关题目
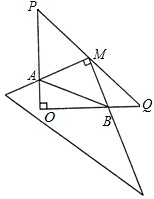
 (2012•南充)在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(2012•南充)在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B. 如图所示,在Rt△POQ中,∠POQ=90°,OP:OQ=3:2,点Q在反比例函数y=
如图所示,在Rt△POQ中,∠POQ=90°,OP:OQ=3:2,点Q在反比例函数y=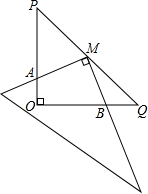 如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.