Question

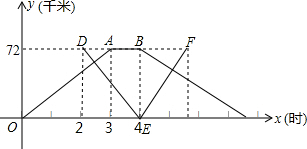
甲乙两个港口相距72千米，一艘轮船从甲港出发，顺流航行3小时到达乙港，休息1小时后立即返回；一艘快艇在轮船出发2小时后由乙港到甲港，并立即返回（掉头时间忽略不计）．已知水流速度是2千米/时，下图表示轮船和快艇距甲港的距离y（千米）与轮船出发时间（小时）之间的函数关系式，结合图象看，快艇出发

 

小时，轮船和快艇在返回途中相距12千米．

Answer 1

考点：一次函数的应用

专题：

分析：先根据题意求出轮船顺流航行的速度，则逆流航行的速度可求，从而得出轮船从乙港返回甲港的时间，得出C点坐标，再根据待定系数法求出BC的解析式，同理先求出快艇的逆流速度，再求出顺流速度，从而得出快艇返回的时间，求出F点坐标，再由待定系数法求出EF的解析式；然后根据返回途中相距12千米，即两个函数的函数值的差是12，则可以列出方程，求得x的值．

解答：解：如图．∵甲乙两个港口相距72千米，一艘轮船从甲港出发，顺流航行3小时到达乙港，
∴轮船顺流航行的速度是：72：3=24千米/时，
∴轮船在静水中的速度是：24-2=22千米/时，逆流航行的速度是：22-2=20千米/时，
∴轮船逆流航行的时间为：72÷20=3.6，
∴C点的横坐标为：4+3.6=7.6，即C（7.6，0）．
设线段BC所在直线的解析式为y=kx+b，
∵B（4，72），C（7.6，0），
∴

4k+b=72   7.6k+b=0

，
解得：

k=-20 b=152

，
∴线段BC的解析式为：y=-20x+152（4≤x≤7.6）．
∵快艇从乙港到甲港用的时间是4-2=2小时，
∴快艇逆流航行的速度为：72÷2=36千米/时，
∴快艇在静水中的速度是：36+2=38千米/时，顺流航行的速度是：38+2=40千米/时，
∴快艇返回的时间是：72÷40=1.8小时，
∴点F的横坐标为：4+1.8=5.8，即F（5.8，72）．
设线段EF所在直线的解析式为y=mx+n，
∵E（4，0），F（5.8，72），
∴

4m+n=0 5.8m+n=72

，
解得 

m=40 n=-160

，
∴线段EF的解析式为y=40x-160（4≤x≤5.8）．
∵轮船和快艇在返回途中相距12千米，
∴40x-160-（-20x+152）=12或-20x+152-（40x-160）=12，
解得：x=5.4或x=5，均符合题意，
∴5-2=3小时和5.4-2=3.4小时，
∴快艇出发3小时或3.4小时两船相距12千米．
故答案为3或3.4．

点评：本题考查了用一次函数解决实际问题，待定系数法求一次函数的解析式，解答时求出一次函数的解析式是解答本题的关键，注意利用数形结合的思想可以加深对题目的理解．