��Ŀ����
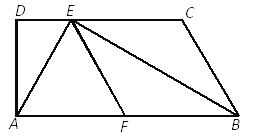
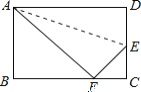
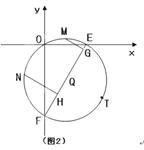
����Ŀ����ͼ1����A��B��P�ֱ������������ϣ���APB=60�㣬PB=m��PA=2m���Ե�PΪԲ�ġ�PBΪ�뾶����P������OBP��ƽ���߷ֱ���P��OP��C��D������AC��
��1����֤��ֱ��AB����P�����ߣ�
��2������ACD�����ΪS����S����m�ĺ�����ϵʽ��
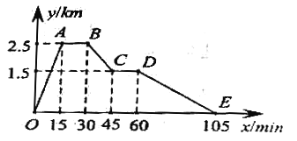
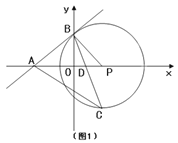
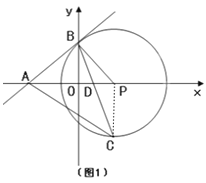
��3����ͼ2����m=2ʱ���ѵ�C����ƽ��һ����λ�õ���T����O��T��������Q��x�ᡢy����E��F���㣬��M��N�ֱ�Ϊ����![]() ���е㣬��MG��EF��NH��EF������ΪG��H������MG+NH��ֵ��
���е㣬��MG��EF��NH��EF������ΪG��H������MG+NH��ֵ��
���𰸡�������
������������: ��1���������ߵ��ж�����֤�á�ABP=90�����ж����ߣ�
��2������PC�����ݡ�APB=90��-��OBP=��OBA����OBC=��PBC���õ���ADB=��PBC+��PBC=��ABD���Ӷ��õ���CPA=��POB=90�������������ε������ʽ�õ�S=![]() m2��
m2��
��3����TJ��x�ᣬTK��y�ᣬ����ET��FT���õ���ETJ�ա�FTK���Ӷ��õ�NH=![]() NR=
NR=![]() OF��MG=
OF��MG=![]() OE��������MG+NH=
OE��������MG+NH=![]() ��OE+OF��=
��OE+OF��=![]() ��4=2.
��4=2.
���:
��1���ߡ�POB=90�㣬��APB=60�㣬
��PB=m��
��PO=![]() PB=
PB=![]() m��OB=
m��OB=![]() m��
m��
�֡�PA=2m��
��OA=![]() m��
m��
��RT��OAB��AB=![]() m
m
��PA2+AB2=PA2
���ABP=90�㣬
��PB�ǡ�P�İ뾶��
��ֱ��AB�ǡ�P�����ߣ�
��2������PC��
�ߡ�APB=90��-��OBP=��OBA����OBC=��PBC��
���ADB=��PBC+��PBC=��ABD
��AD=AB=![]() m��
m��
�֡�PB=PC=m��
��PC��OC
���CPA=��POB=90�㣬
��S��ACD=![]() AD��CP=
AD��CP=![]()
![]() m��m=
m��m=![]() m2��
m2��
��3����TG��x�ᣬTK��y�ᣬ����ET��FT��
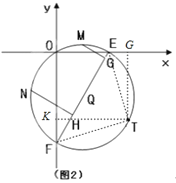
��m=2ʱ��PO=![]() m���ɣ�2��֪��CPA=90�㣬
m���ɣ�2��֪��CPA=90�㣬
��C��Ϊ ��1��-2����
��T��2��-2����TG=TK=2��
���T�ڡ�EOF��ƽ�����ϣ���![]()
��TE=TF��
���ETG�ա�FTK��
��EF=EG��
��OE+OF=OG-EG+OK+FK=OG+OK=4
�ӳ�NH����Q��R������QN��QR���ߡ�EOF=90�㣬
��EFΪ��Q��ֱ������![]()
![]()
![]()
��NR=OF
��NH=![]() NR=
NR=![]() OF
OF
ͬ��MG=![]() OE
OE
��MG+NH=![]() ��OE+OF��=
��OE+OF��=![]() ��4=2
��4=2
�㾦: ���⿼����Բ���ۺ�֪ʶ���ѶȽϴ�һ��Ϊ�п����ѹ����.