题目内容
 等腰梯形ABCD的对角线AC、BD相交于点O,则图中共有________对全等三角形,有________个等腰三角形.
等腰梯形ABCD的对角线AC、BD相交于点O,则图中共有________对全等三角形,有________个等腰三角形.
3 2
分析:根据等腰梯形的性质即可得出AB=CD,AO=DO B0=CO,AD=AD,BD=AC,AB=CD,根据全等三角形的判定和等腰三角形的判定定理即可求解.
解答:等腰梯形ABCD的对角线AC、BD相交于点O,
∴AB=CD,AO=DO B0=CO,
∴△AOB≌△COD,
∴△AOD与△BOC均为等腰三角形,
∵AC=BD,BC=BC,
∴△ABC≌△BCD,
∵AD=AD,BD=AC,AB=CD,
∴△ABD≌△ACD,
故有三对全等三角形,两个等腰三角形.
故答案为:3,2.
点评:本题考查了等腰梯形的性质及全等三角形的判定与等腰三角形的判定,难度一般,关键是掌握全等三角形的判定定理.
分析:根据等腰梯形的性质即可得出AB=CD,AO=DO B0=CO,AD=AD,BD=AC,AB=CD,根据全等三角形的判定和等腰三角形的判定定理即可求解.
解答:等腰梯形ABCD的对角线AC、BD相交于点O,
∴AB=CD,AO=DO B0=CO,
∴△AOB≌△COD,
∴△AOD与△BOC均为等腰三角形,
∵AC=BD,BC=BC,
∴△ABC≌△BCD,
∵AD=AD,BD=AC,AB=CD,
∴△ABD≌△ACD,
故有三对全等三角形,两个等腰三角形.
故答案为:3,2.
点评:本题考查了等腰梯形的性质及全等三角形的判定与等腰三角形的判定,难度一般,关键是掌握全等三角形的判定定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 16、如图,等腰梯形ABCD的对角线AC、BD相交于O,则图中共有全等三角形( )
16、如图,等腰梯形ABCD的对角线AC、BD相交于O,则图中共有全等三角形( ) 7、等腰梯形ABCD的对角线AC、BD相交于点O,则图中共有
7、等腰梯形ABCD的对角线AC、BD相交于点O,则图中共有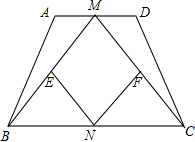 如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点.
如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点. 等腰梯形ABCD中,AD∥BC,AB=CD,BD为对角线,将△ABD沿BD对折,A点刚好落在BC边的Aˊ处,∠C=60°,BC=12,则等腰梯形ABCD的周长为=
等腰梯形ABCD中,AD∥BC,AB=CD,BD为对角线,将△ABD沿BD对折,A点刚好落在BC边的Aˊ处,∠C=60°,BC=12,则等腰梯形ABCD的周长为=