题目内容
 等腰梯形ABCD中,AD∥BC,AB=CD,BD为对角线,将△ABD沿BD对折,A点刚好落在BC边的Aˊ处,∠C=60°,BC=12,则等腰梯形ABCD的周长为=
等腰梯形ABCD中,AD∥BC,AB=CD,BD为对角线,将△ABD沿BD对折,A点刚好落在BC边的Aˊ处,∠C=60°,BC=12,则等腰梯形ABCD的周长为=30
30
.分析:根据等腰梯形的性质,∠A=180°-60°,根据翻折变换的性质,∠A=∠BA′D,得出∠DA′C=∠C=60°,△DA′C为等边三角形,AB=AD=CD=
BC,继而即可求出等腰梯形ABCD的周长.
| 1 |
| 2 |
解答:解:根据等腰梯形的性质,∠A=180°-60°,
根据翻折变换的性质,∠A=∠BA′D,
∴∠DA′C=∠C=60°,△DA′C为等边三角形,
∴AB=AD=CD=
BC=6,
∴等腰梯形ABCD的周长为:AB+BC+CD+DA=6+6+6+12=30.
故答案为:30.
根据翻折变换的性质,∠A=∠BA′D,
∴∠DA′C=∠C=60°,△DA′C为等边三角形,
∴AB=AD=CD=
| 1 |
| 2 |
∴等腰梯形ABCD的周长为:AB+BC+CD+DA=6+6+6+12=30.
故答案为:30.
点评:本题考查翻折变换的知识及等腰梯形的性质,解题关键是得出△DA′C为等边三角形,AB=AD=CD=
BC,难度一般.
| 1 |
| 2 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

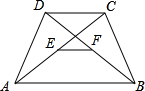 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°, 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是