Question

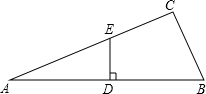如图：△ABC中，∠C=90°，tanA=

1

2

，DE是AB的垂直平分线，BC=2．求：（1）sin∠AED的值；（2）CE的长．

Answer 1

分析：此题给出了两个直角三角形，在这两个直角三角形中又给出了一边一函数值，这就可以利用这些已知条件解直角三角形了．

解答：解：（1）∵∠C=90°，tanA=

1

2

，BC=2，
∴AC=4，
AB=

16+4

=2

5

，
∵ED⊥AB，
∴sin∠AED=sinB=

AC

AB

=

2 5

5

；

（2）方法一：∵sin∠AED=

AD

AE

，
∴

2 5

5

=

5

AE

，
∴AE=

5

2

，
∴CE=4-

5

2

=

3

2

；
方法二：∵∠A=∠A，∠C=∠ADE
∴△ADE∽△ACB
∵AE=4-CE
∴

4-CE

2 5

=

5

4

∴CE=

3

2

．

点评：解直角三角形时学生一定要对直角三角形中的边角关系掌握好，即sinA=a：c=cosB，sinB=b：c=cosA，
tanA=a：b=cotB，tanB=b：a=cotA．此外注意还要利用勾股定理．