题目内容
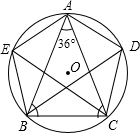已知：如图，△ABC是⊙O的内接等腰三角形，顶角∠BAC=36°，弦BD、CE分别平分∠ABC、∠ACB．求证：五边形AEBCD是正五边形．
分析：求证五边形AEBCD是正五边形，就是证明这个五边形的五条边所对的弧相等．
解答：证明：∵AB=AC，
∴∠ABC=∠ACB，
又∵∠BAC=36°，
∴∠ABC=∠ACB=72°．
又∵BD、CE平分∠ABC、∠ACB．
∴∠BAC=∠BCE=∠ACE=∠ABD=∠DBC=36°，
∴
=
=
=
=
．
易证五边形AEBCD为正五边形．
∴∠ABC=∠ACB，
又∵∠BAC=36°，
∴∠ABC=∠ACB=72°．
又∵BD、CE平分∠ABC、∠ACB．
∴∠BAC=∠BCE=∠ACE=∠ABD=∠DBC=36°，
∴
 |
| AE |
|
| BE |
|
| BC |
|
| CD |
|
| DA |
易证五边形AEBCD为正五边形．
点评：本题主要考查了连接圆的等分点所得到的多边形是正多边形这一结论．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
17、已知，如图，△ABC中，∠BAC=90°，AD⊥BC于点D，BE平分∠ABC，交AD于点M，AN平分∠DAC，交BC于点N．
已知：如图，∠ABC、∠ACB 的平分线相交于点F，过F作DE∥BC于D，交AC 于E，且AB=6，AC=5，求三角形ADE的周长．
已知：如图，△ABC是等边三角形，点D在AB上，点E在AC的延长线上，且BD=CE，DE交BC于F，求证：BF=CF+CE．
已知：如图，△ABC中，AB=AC=10，BC=16，点D在BC上，DA⊥CA于A．
已知：如图，△ABC中，AD⊥BC，BD=DE，点E在AC的垂直平分线上．