Question

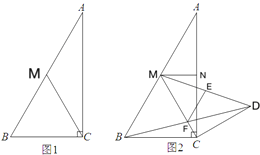
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=30°，点M是AB边的中点.

(1)如图1，若CM=，求△ACB的周长；

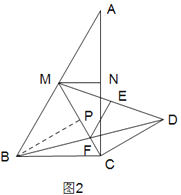
(2)如图2，若N为AC的中点，将线段CN以C为旋转中心顺时针旋转60°，使点N至点D处，连接BD交CM于点F，连接MD，取MD的中点E，连接EF.求证：3EF=2MF.

Answer 1

【答案】(1)；(2)证明见解析.

【解析】

（1）根据直角三角形中，斜边上的中线等于斜边的一半可得AB的长度，根据30°所对的直角边等于斜边的一半可得BC的长度，最后根据勾股定理可得AC的长度，计算出周长即可；

（2）如图所示添加辅助线，由（1）可得ΔBCM是等边三角形，可证ΔBCP≌ΔCMN，进而证明ΔBPF≌ΔDCF，根据E是MD中点，得出，根据BPMC，得出，进而得出3EF=2MF即可．

解：(1) 在Rt△ABC中，∠ACB=90°，点M是AB边的中点，

∴

∴AB=2MC=，

又∵∠A=30°，

∴

由勾股定理可得，

∴△ABC的周长为++6=

(2)过点B作BPMC于P

∵∠ACB=90°，∠A=30° ，

∴

∵M为AB的中点 ，

∴

∴

∵∠ABC=60°

∴ΔBCM是等边三角形

∴∠CBP=∠MCN=30°,BC=CM

∴在ΔBCP与ΔCMN中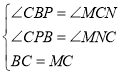

∴ΔBCP≌ΔCMN(AAS)

∴BP=CN ∵ CN=CD ∴BP=CD

∵∠BPF=∠DCF=90°

∠BFP=∠DFC

∴ΔBPF≌ΔDCF

∴PF=FC BF=DF

∵E是MD中点，

∴

∵BPMC，

∴

∴，

∴

∴