Question

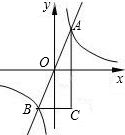
在直角坐标系xOy中，直线y=-x+3与双曲线y=

1

3x

围成的区域记为S．将1、2、3、-1、-2、-3六个数中任意一个数作为M的横坐标，它的倒数作为M的纵坐标，则M在S内（不含边界）的概率是

 

．

Answer 1

分析：求出x取每个数值时，对应的一次函数与反比例函数的函数值，M的纵坐标如果大于反比例函数上对应点的纵坐标而小于一次函数对应的点的纵坐标，则M就在S内，即可判断6个点中在S的范围内的点的个数，从而求解．

解答：解：当x=1时，y=-x+3=2，y=

1

3x

=

1

3

，1的倒数是1，且

1

3

＜1＜2，故M在S内；
当x=2时，y=-x+3=1，y=

1

3x

=

1

6

，2的倒数是

1

2

，且

1

6

＜

1

2

＜1，故M在S内；
当x=3时，y=-x+3=0，y=

1

3x

=

1

9

，3的倒数是

1

3

，且

1

3

＞0且

1

3

＞

1

9

，故不M在S内；
当x=-1时，y=-x+3=4，y=

1

3x

=-

1

3

，-1的倒数是-1，且-1＜-

1

3

＜4故不M在S内；
当x=-2时，y=-x+3=1，y=

1

3x

=-

1

6

，-2的倒数是-

1

2

，且-

1

2

＜-

1

6

＜1故不M在S内；
当x=3-时，y=-x+3=0，y=

1

3x

=-

1

9

，-3的倒数是-

1

3

，且-

1

3

＜-

1

9

＜0故不M在S内．
则在S的范围内的有2个．
故M在S内（不含边界）的概率是

2

6

=

1

3

．
故答案是：

1

3

．

点评：本题主要考查了列举法求概率，正确理解M在S范围内的条件是解题的关键．